Für eine skalare Funktion 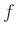 bezeichnet man
bezeichnet man 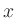 als kritischen Punkt, wenn
grad
als kritischen Punkt, wenn
grad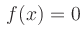 . Ist
. Ist 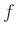 zweimal stetig differenzierbar, so wird
der Typ des kritischen Punktes, d.h. die
Form des Funktionsgraphen in einer Umgebung von
zweimal stetig differenzierbar, so wird
der Typ des kritischen Punktes, d.h. die
Form des Funktionsgraphen in einer Umgebung von 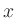 , durch die Hesse-Matrix
bestimmt. Je nach Vorzeichen der Eigenwerte
, durch die Hesse-Matrix
bestimmt. Je nach Vorzeichen der Eigenwerte 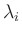 von
von
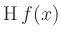 unterscheidet man zwischen
unterscheidet man zwischen
- Flachpunkt:
Alle Eigenwerte
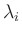 sind Null.
sind Null.
- elliptischer Punkt:
Alle Eigenwerte
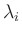 sind ungleich Null
und haben das gleiche Vorzeichen.
Die Funktion
sind ungleich Null
und haben das gleiche Vorzeichen.
Die Funktion 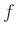 hat in diesem Fall ein lokales Extremum bei
hat in diesem Fall ein lokales Extremum bei 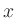 .
.
- hyperbolischer Punkt:
Es gibt Eigenwerte
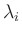 mit verschiedenem
Vorzeichen. Man bezeichnet
mit verschiedenem
Vorzeichen. Man bezeichnet 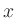 auch als Sattelpunkt.
auch als Sattelpunkt.
- parabolischer Punkt:
Mindestens ein Eigenwert
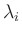 ist Null, und alle
anderen Eigenwerte haben das gleiche Vorzeichen.
ist Null, und alle
anderen Eigenwerte haben das gleiche Vorzeichen.
Die Bezeichnungen sind durch die Form der Höhenlinien im bivariaten Fall
motiviert, wie dies in der Abbildung illustriert ist.
![\includegraphics[width=0.3\linewidth]{kritischer_punkt_elliptisch}](/inhalt/aussage/aussage683/img6.png) |
![\includegraphics[width=0.3\linewidth]{kritischer_punkt_hyperbolisch}](/inhalt/aussage/aussage683/img7.png) |
![\includegraphics[width=0.3\linewidth]{kritischer_punkt_parabolisch}](/inhalt/aussage/aussage683/img8.png) |
| elliptischer Punkt |
hyperbolischer Punkt |
parabolischer Punkt |
Bei Funktionen in zwei Veränderlichen kann der Typ anhand der
Determinante der Hesse-Matrix klassifiziert werden. Ist
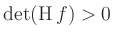 (
(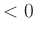 ), so handelt es sich
um ein Extremum (einen Sattelpunkt). Für ein Minimum bzw. ein Maximum ist
), so handelt es sich
um ein Extremum (einen Sattelpunkt). Für ein Minimum bzw. ein Maximum ist
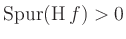 bzw.
bzw. 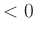 . Verschwindet die Determinante und ist die Hesse-Matrix nicht
Null, so ist der Punkt parabolisch.
. Verschwindet die Determinante und ist die Hesse-Matrix nicht
Null, so ist der Punkt parabolisch.
Es werden die kritischen Punkte der Funktion
sowie deren Typ bestimmt.
Dazu werden zunächst Gradient und Hesse-Matrix gebildet:
Aus der Bedingung
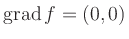 t für kritische
Punkte erhält man
t für kritische
Punkte erhält man
und damit die kritischen Punkte
Die entsprechenden Hesse-Matrizen sind
Zur Bestimmung des Typs werden Determinante und Spur gebildet.
Alternativ lässt sich der Typ der kritischen Punkte anhand der
Nullstellenmenge von 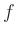 und der sich daraus ergebenden Vorzeichenverteilung
bestimmen.
und der sich daraus ergebenden Vorzeichenverteilung
bestimmen.
Sattelpunkte von 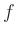 sind die Schnittpunkte der Nullstellenmenge
mit Vorzeichenwechsel von
sind die Schnittpunkte der Nullstellenmenge
mit Vorzeichenwechsel von 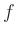 .
Lokale Extrema befinden sich in
von der Nullstellenmenge eingeschlossenen beschränkten Bereichen.
Ist
.
Lokale Extrema befinden sich in
von der Nullstellenmenge eingeschlossenen beschränkten Bereichen.
Ist 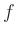 in einem solchen Bereich positiv, muss dort mindestens ein
Maximum existieren, andernfalls mindestens ein Minimum.
in einem solchen Bereich positiv, muss dort mindestens ein
Maximum existieren, andernfalls mindestens ein Minimum.
(Inhalt vorübergehend nicht verfügbar)
| |
automatisch erstellt
am 5.1.2017 |


![\includegraphics[width=0.3\linewidth]{kritischer_punkt_elliptisch}](/inhalt/aussage/aussage683/img6.png)
![\includegraphics[width=0.3\linewidth]{kritischer_punkt_hyperbolisch}](/inhalt/aussage/aussage683/img7.png)
![\includegraphics[width=0.3\linewidth]{kritischer_punkt_parabolisch}](/inhalt/aussage/aussage683/img8.png)
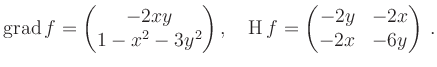
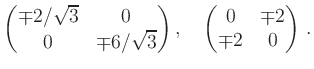
![]() und der sich daraus ergebenden Vorzeichenverteilung
bestimmen.
und der sich daraus ergebenden Vorzeichenverteilung
bestimmen.
![\includegraphics[width=0.7\linewidth]{vorzeichenverteilung_kreis_xachse}](/inhalt/beispiel/beispiel1312/img16.png)