Mathematik-Online-Kurs: Differentialgleichungen-Differentialgleichungssysteme-Lineare Systeme-Klassifizierung reeller zweidimensionaler Differentialgleichungssysteme mit konstanten Koeffizienten

	[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
	Mathematik-Online-Kurs: Differentialgleichungen - Differentialgleichungssysteme - Lineare Systeme
	Klassifizierung reeller zweidimensionaler Differentialgleichungssysteme mit konstanten Koeffizienten

Das qualitative Verhalten der Lösungen des Differentialgleichungssystems

$\displaystyle u^\prime = A u,\quad u = (u_1,u_2)^{\operatorname t}\,,$

mit

einer reellen $2 \times 2$ -Matrix lässt sich anhand der Jordan-Normalform

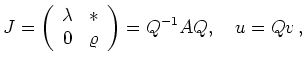
$\displaystyle J = \left(\begin{array}{cc} \lambda & * \\ 0 & \varrho \end{array}\right) = Q^{-1} A Q,\quad u = Qv \,,$

von

klassifizieren. Die Abbildungen zeigen dabei jeweils den Verlauf typischer Lösungskurven des transformierten Systems

Instabiler Sattel: $\lambda\varrho<0$

$\includegraphics[width=0.45\linewidth]{sattel.eps}$
Knoten: $\lambda\varrho>0$ , $\lambda,\varrho\in\mathbb{R}$

$\includegraphics[width=0.45\linewidth]{knoten1.eps}$ $\includegraphics[width=0.45\linewidth]{knoten2.eps}$

stabil, $\lambda,\varrho<0$ instabil, $\lambda,\varrho>0$

Existiert keine Basis aus Eigenvektoren von , so spricht man von einem entarteten Knoten.

$\includegraphics[width=0.45\linewidth]{knoten3.eps}$ $\includegraphics[width=0.45\linewidth]{knoten4.eps}$

stabil, $\lambda<0$ instabil, $\lambda>0$
Spirale: $\lambda=r+\mathrm{i}\omega=\bar\varrho$ , $r\omega\ne 0$

$\includegraphics[width=0.45\linewidth]{spirale1.eps}$ $\includegraphics[width=0.45\linewidth]{spirale2.eps}$

stabil, instabil,
Zentrum: $\lambda=\mathrm{i}\omega=\bar\varrho$ , $\omega\ne 0$

$\includegraphics[width=0.45\linewidth]{zentrum.eps}$

Zusätzlich gibt es noch degenerierte Fälle, bei denen ein Eigenwert null ist.

$\includegraphics[width=0.3\moimagesize]{entart1.eps}$		$\includegraphics[width=0.3\moimagesize]{entart2.eps}$		$\includegraphics[width=0.3\moimagesize]{entart3.eps}$
$\lambda=0$ , $\varrho<0$		$\lambda=0$ , $\varrho>0$		$\lambda=0$ , $\varrho=0$ , $A\ne 0$

In jedem dieser Fälle hat das Differentialgleichungssystem Ruhepunkte entlang der gesamten -Achse.

(Inhalt vorübergehend nicht verfügbar)

automatisch erstellt am 6.6.2011

$\includegraphics[width=0.45\linewidth]{knoten1.eps}$	$\includegraphics[width=0.45\linewidth]{knoten2.eps}$
stabil, $\lambda,\varrho<0$	instabil, $\lambda,\varrho>0$

$\includegraphics[width=0.45\linewidth]{knoten3.eps}$	$\includegraphics[width=0.45\linewidth]{knoten4.eps}$
stabil, $\lambda<0$	instabil, $\lambda>0$

$\includegraphics[width=0.45\linewidth]{spirale1.eps}$	$\includegraphics[width=0.45\linewidth]{spirale2.eps}$
stabil,	instabil,