Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Mehrdimensionale Integration - Transformation mehrdimensionaler Integrale

Volumenelement in Kugelkoordinaten

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Für die Koordinatentransformation

$\displaystyle x = r\sin\vartheta\cos\varphi,\quad y = r\sin\vartheta\sin\varphi,\quad z = r\cos\vartheta $

ist

$\displaystyle dx\,dy\,dz = r^2 \sin\vartheta\,dr\,d\vartheta\,d\varphi \,. $

Insbesondere gilt damit für das Integral einer Funktion $ f$ auf einer Kugel $ K: \; 0 \le r \le R$

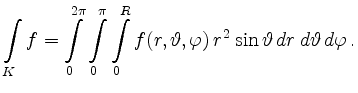
$\displaystyle \int\limits_K f = \int\limits_0^{2 \pi}\int\limits_0^{\pi} \int\l... ..._0^{R} f(r,\vartheta,\varphi)\,r^2 \sin\vartheta\,dr\,d\vartheta\,d\varphi \,. $

Speziell ist für eine radialsymmetrische Funktiopn $ f(r)$

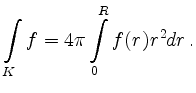
$\displaystyle \int\limits_K f = 4\pi \int\limits_0^R f(r) r^2 dr\,. $

(Inhalt vorübergehend nicht verfügbar)

(Inhalt vorübergehend nicht verfügbar)
Der Druck in der Höhe $ h$ über Nullniveau wird durch die barometrische Höhenformel bestimmt:

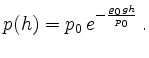
$\displaystyle p(h)=p_0 \,e^{-\frac{\varrho_0 g h}{p_0}} \,. $

Dabei sind $ p_0 = 101300 \frac{\text{N}}{\text{m}^2}$ der Normaldruck, $ \varrho_0 = 0.150 \frac{\text{kg}}{\text{m}^3}$ die Sauerstoffdichte auf Nullniveau (21% der Luft sind Sauerstoff) und $ g = 9,80 \frac{\text{m}}{\text{s}^2}$ die Erdbeschleunigung.

Die Dichte ist mit dem Druck über die ideale Gasgleichung verknüpft:

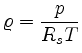
$\displaystyle \varrho = \frac {p}{R_s T} $

mit $ R_s = \frac{k_B}{m_{\text{Molekül}}} = 519 \frac{\text{N\,m}}{\text{K\,kg}}$ der spezifischen Gaskonstante für Sauerstoff und $ T$ der in Kelvin gemessenen Temperatur. Der Einfachheit halber wird diese als konstant $ -3°C$, also $ T=270$   K, angenommen.

Aus den beiden Gleichungen läßt sich die Gesamtmasse des Sauerstoffs in der Atmosphäre näherungsweise berechnen:

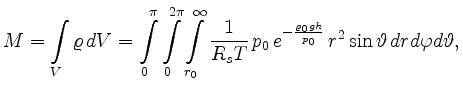
$\displaystyle M=\int\limits_V \varrho\, dV = \int\limits_0^\pi \int\limits_0^{2... ...0\,e^{-\frac{\varrho_0 g h}{p_0}}\, r^2\sin\vartheta\,dr d\varphi d\vartheta, $

wobei $ r_0=6.37\cdot 10^6$m der Erdradius ist. Nach Substitution von $ h=r-r_0$ und Integration über $ \vartheta$ und $ \varphi$ ergibt sich

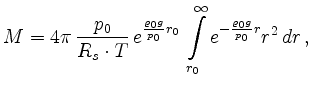
$\displaystyle M=4\pi \, \frac{p_0}{R_s\cdot T} \, e^{\frac{\varrho_0 g}{p_0}r_0} \, \int\limits_{r_0}^\infty e^{-\frac{\varrho_0 g}{p_0}r}r^2\, dr \,, $

und mit zweifacher partieller Integration folgt für das Integral

$\displaystyle \int\limits_{r_0}^\infty e^{-cr}r^2\,dr = \left[-\frac{r^2}{c}e^... ...^{-cr}\right]_{r_0}^\infty + \left[-\frac{2}{c^3}e^{-cr}\right]_{r_0}^\infty $

( $ c = \frac{\varrho_0 g}{p_0}$). Insgesamt erhält man also

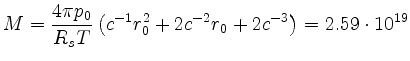$\displaystyle M = \frac{4\pi p_0}{R_s T} \left( c^{-1} r_0^2 + 2 c^{-2} r_0 + 2 c^{-3} \right) = 2.59 \cdot 10^{19}$kg$\displaystyle \,. $

Zum Vergleich:
- Erdmasse: $ 6\cdot10^{24}$kg $ (2.3\cdot 10^5\,M)$
- Mondmasse: $ 7.4\cdot 10^{22}$kg $ (2.9\cdot 10^3\,M)$

(Autor: Mirjam Beuttler)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.1.2017