Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Vektoranalysis - Integration - Kurvenintegrale

Arbeitsintegral

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Für einen Weg $ {C}$ mit regulärer Parametrisierung

$\displaystyle [a,b] \ni t \mapsto \vec{r }(t) = \left(\begin{array}{c}x(t)\\ y(t)\\ z(t) \end{array}\right) $

und ein Vektorfeld $ \vec{F}(x,y,z)$ wird mit

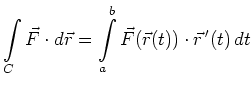
$\displaystyle \int\limits_C \vec{F}\cdot d\vec{r}=\int\limits_a^b \vec{F}(\vec{r}(t))\cdot \vec{r}\,'(t)\,dt $

das Arbeitsintegral bezeichnet.

\includegraphics[width=.5\linewidth]{a_arbeitsintegral_bild}

Es entspricht dem Kurvenintegral der Projektion von $ \vec{F}$ in tangentialer Richtung,

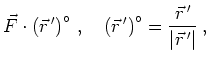
$\displaystyle \vec{F}\cdot \left(\vec{r}\,'\right)^\circ \,,\quad \left(\vec{r}\,'\right)^\circ = \frac{ \vec{r}\,'}{\vert\vec{r}\,'\vert} \,, $

und ist unabhängig von der Parametrisierung bei gleichbleibender Orientierung des Weges. Bei Umkehrung der Durchlaufrichtung ändert sich das Vorzeichen des Integrals.

In Komponentenschreibweise hat das Arbeitsintegral die Form

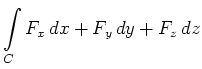
$\displaystyle \int\limits_C F_x\,dx + F_y\,dy+F_z\,dz $

mit $ dx=x'(t)\,dt\,,\,dy=y'(t)\,dt\,,\, dz=z'(t)\,dt$.
Beim Durchlaufen des Viertelkreises

\begin{displaymath} \vec{r}(t)=\left( \begin{array}{c} \cos t \\ \sin t\\ \end{array}\right),\quad t\in [0,\pi/2]\,, \end{displaymath}

im Kraftfeld

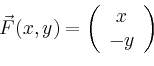
\begin{displaymath} \vec{F}(x,y)=\left( \begin{array}{c} x\\ -y\\ \end{array}\right) \end{displaymath}

wird die Arbeit

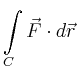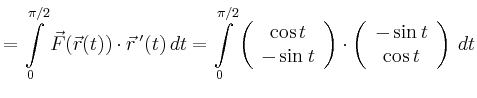$\displaystyle \int\limits_C \vec{F}\cdot d\vec{r}$ $\displaystyle = \int\limits_0^{\pi/2} \vec{F}(\vec{r}(t))\cdot \vec{r}\,'(t)\,d... ...\right)\cdot\left( \begin{array}{c} -\sin t \\ \cos t \\ \end{array}\right)\,dt$    
  $\displaystyle = \int\limits_0^{\pi/2} -2\cos t \sin t \,dt = \left[\cos^2 t \right]_0^{\pi/2} = -1$    

verrichtet.
Die in einem Kraftfeld $ \vec{F}$ entlang eines Geradenstücks

$\displaystyle C:\ t \mapsto \vec{r}(t) = \vec{p} + t\vec{d},\quad t\in [a,b]\,, $

verrichtete Arbeit ist

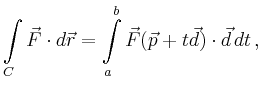
$\displaystyle \int\limits_C \vec{F}\cdot d\vec{r} = \int\limits_a^b \vec{F}(\vec{p}+t\vec{d})\cdot \vec{d}\,dt\,, $

wobei $ \vec{r}\,'(t) = \vec{d}\,.$

Beispielsweise ist für

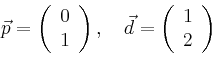
\begin{displaymath} \vec{p}=\left( \begin{array}{c} 0\\ 1\\ \end{array}\right),\quad \vec{d}=\left( \begin{array}{c} 1\\ 2\\ \end{array}\right) \end{displaymath}

mit $ t\in[a,b]=[0,3]$ und

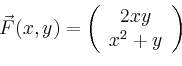
\begin{displaymath} \vec{F}(x,y)=\left( \begin{array}{c} 2xy\\ x^2+y\\ \end{array}\right) \end{displaymath}

die verrichtete Arbeit

\begin{displaymath} \int\limits_0^3 \left( \begin{array}{c} 2t(2t+1)\\ t^2+2t+1\... ...imits_0^3 6t^2+6t+2\,dt = \left[ 2t^3+3t^2+2t\right]_0^3=87\,. \end{displaymath}

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 9.10.2013