Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Vektoranalysis - Integration - Flächenintegrale

Flussintegral

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Der Fluss eines stetigen Vektorfeldes $ \vec{F}(x,y,z)$ durch eine Fläche $ {S}$ mit regulärer Parametrisierung

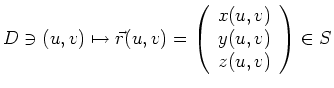
$\displaystyle D\ni (u,v) \mapsto \vec{r}(u,v) = \left(\begin{array}{c}x(u,v)\\ y(u,v)\\ z(u,v) \end{array}\right) \in {S} $

in Richtung der Normalen

$\displaystyle \vec{n} = \partial_u \vec{r} \times \partial_v \vec{r} $

ist

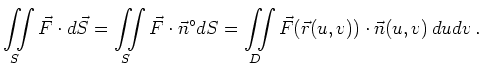
$\displaystyle \iint\limits_{S} \vec{F} \cdot d\vec{S} = \iint\limits_{S} \vec{F... ...n}^\circ dS = \iint\limits_D \vec{F}(\vec{r}(u,v)) \cdot \vec{n}(u,v)\,dudv\,. $

Man bezeichnet dabei

$\displaystyle d\vec{S} = \vec{n}^\circ dS\,,\quad dS = \vert\vec{n}(u,v)\vert\, dudv\,, $

als vektorielles Flächenelement.

Bei gleicher Orientierung des Normalenvektors ist das Flussintegral unabhängig von der gewählten Parametrisierung. Die Umkehrung der Normalenrichtung bewirkt eine Änderung des Vorzeichens.

\includegraphics[width=.6\linewidth]{a_flussintegral_bild}

Die Glattheitsvoraussetzungen an $ \vec{F}$ und $ \vec{r}(u,v)$ können abgeschwächt werden, indem man das Integral über einen geeigneten Grenzprozess definiert.

Es soll der Fluss des Vektorfeldes

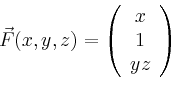
\begin{displaymath} \vec{F}(x,y,z)=\left( \begin{array}{c} x\\ 1\\ yz\\ \end{array}\right) \end{displaymath}

durch die Fläche

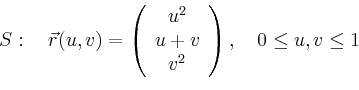
\begin{displaymath} S:\quad \vec{r}(u,v)=\left( \begin{array}{c} u^2 \\ u+v\\ v^2\\ \end{array}\right),\quad 0\leq u,v \leq 1 \end{displaymath}

berechnet werden.

Die partiellen Ableitungen in $ u$- und $ v$-Richtung sind

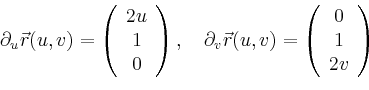
\begin{displaymath} \partial_u \vec{r}(u,v)=\left( \begin{array}{c} 2u\\ 1\\ 0\\... ...(u,v)=\left( \begin{array}{c} 0\\ 1\\ 2v\\ \end{array}\right) \end{displaymath}

und damit

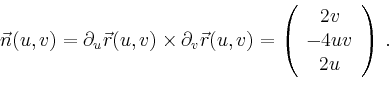
\begin{displaymath} \vec{n}(u,v) = \partial_u \vec{r}(u,v)\times \partial_v \ve... ...left( \begin{array}{c} 2v\\ -4uv\\ 2u\\ \end{array}\right)\,. \end{displaymath}

Für das Flussintegral ergibt sich also

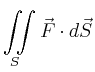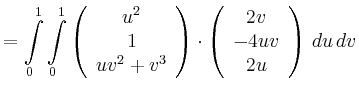$\displaystyle \iint\limits_{S} \vec{F} \cdot d\vec{S}$ $\displaystyle =\int\limits_0^1\int\limits_0^1 \left( \begin{array}{c} u^2\\ 1\\... ...\right)\cdot\left( \begin{array}{c} 2v\\ -4uv\\ 2u\\ \end{array}\right)\,du\,dv$    
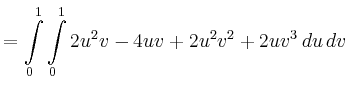  $\displaystyle =\int\limits_0^1\int\limits_0^1 2u^2v-4uv+2u^2v^2+2uv^3 \,du\,dv$    
  $\displaystyle = \int\limits_0^1 \left[ \frac{2}{3}u^3v-2u^2v+\frac{2}{3}u^3v^2+u^2v^3 \right]_0^1\, dv$    
  $\displaystyle = \int\limits_0^1-\frac{4}{3}v+\frac{2}{3}v^2+v^3\,dv = \left[-\frac{2}{3}v^2+\frac{2}{9}v^3+\frac{1}{4}v^4\right]_0^1$    
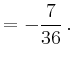  $\displaystyle =-\frac{7}{36}\,.$    

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 9.10.2013