Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Vektoranalysis - Integration - Flächenintegrale

Fluss durch einen Zylindermantel

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Der Fluss eines Feldes

$\displaystyle \vec{F}(\varrho,\varphi,z) = F_\varrho \vec{e}_\varrho + F_\varphi \vec{e}_\varphi + F_z \vec{e}_z $

nach außen durch den Mantel eines Zylinders mit Randkurve $ \varrho=\varrho(\varphi)$ ist

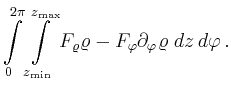
$\displaystyle \int\limits_0^{2\pi}\int\limits_{z_{\min}}^{z_{\max}} F_\varrho \varrho- F_\varphi \partial_\varphi \varrho \,\,dz\,d\varphi \,. $

Der Fluss des Feldes durch eine Rotationsfläche, die durch Drehung der Kurve $ \varrho=\varrho(z)$ um die $ z$-Achse entsteht, ist

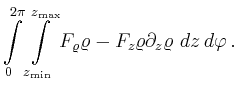
$\displaystyle \int\limits_0^{2\pi}\int\limits_{z_{\min}}^{z_{\max}} F_\varrho \varrho- F_z \varrho \partial_z \varrho \,\,dz\,d\varphi \,. $

Der Fluss durch den Mantel eines Kreiszylinders mit $ \varrho=a$ ist demnach

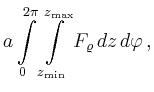
$\displaystyle a\int\limits_0^{2\pi}\int\limits_{z_{\min}}^{z_{\max}} F_\varrho\,dz\,d\varphi \,, $

d.h. nur die axialsymmetrische Komponente des Feldes liefert einen Beitrag. Insbesondere ist beim Kreiszylinder der Fluss für ein axialsymmetrisches Feld $ \vec{F}= f(\varrho) \vec{e}_\varrho$ gleich $ 2\pi a (z_{\max}-z_{\min}) f(a)$.
Die Mantelfläche kann mit Hilfe von Zylinderkoordinaten parametrisiert werden,

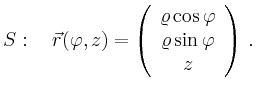
$\displaystyle S:\quad \vec{r}(\varphi,z)=\left(\begin{array}{c} \varrho \cos \varphi \\ \varrho \sin \varphi \\ z \end{array}\right)\,. $

Für $ \varrho=\varrho(\varphi)$ ist die Flächennormale
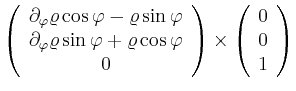$\displaystyle \vec{n}(\varphi,z) = \partial_\varphi \vec{r} \times \partial_z \vec{r}$ $\displaystyle =$ $\displaystyle \left(\begin{array}{c} \partial_\varphi \varrho \cos \varphi - \v... ...{array}\right) \times \left(\begin{array}{c} 0\\ 0\\ 1 \\ \end{array}\right)$  
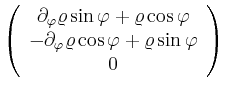  $\displaystyle =$ $\displaystyle \left(\begin{array}{c} \partial_\varphi \varrho \sin \varphi + \v... ...\varphi \varrho \cos \varphi + \varrho \sin \varphi\\ 0 \\ \end{array}\right)$  
  $\displaystyle =$ $\displaystyle -\partial_\varphi \varrho \vec{e}_\varphi+ \varrho \vec{e}_\varrho\,,$  

und das Skalarprodukt mit dem Vektorfeld mit den Komponenten $ F_\varrho, F_\varphi, F_z$ ergibt aufgrund der Orthogonalität der Basisvektoren

$\displaystyle \vec{F} \cdot \vec{n} = F_\varrho \varrho- F_\varphi \partial_\varphi \varrho\,. $

Ist $ \varrho=\varrho(z)$ von $ z$ abhängig, so ergibt sich entsprechend

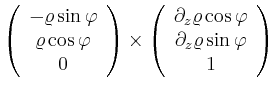$\displaystyle \vec{n}(\varphi,z) = \partial_\varphi \vec{r} \times \partial_z \vec{r}$ $\displaystyle =$ $\displaystyle \left(\begin{array}{c} - \varrho \sin \varphi\\ \varrho \cos \va... ...rho \cos \varphi\\ \partial_z \varrho \sin \varphi\\ 1 \\ \end{array}\right)$  
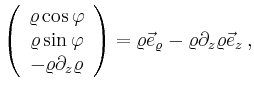  $\displaystyle =$ $\displaystyle \left(\begin{array}{c} \varrho \cos \varphi\\ \varrho \sin \varp... ...ray}\right) = \varrho \vec{e}_\varrho - \varrho \partial_z \varrho \vec{e}_z\,,$  

und das Skalarprodukt mit dem Vektorfeld ist

$\displaystyle \vec{F}\cdot \vec{n} = F_\varrho \varrho- F_z \varrho\partial_z \varrho\,. $

Für den Kreiszylinder ist $ \varrho$ konstant, und somit fallen die Terme, in denen eine Ableitung von $ \varrho$ vorkommt, weg.

Es soll der Fluss des Feldes

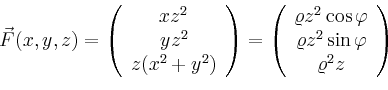
\begin{displaymath} \vec{F}(x,y,z)=\left( \begin{array}{c} xz^2\\ yz^2\\ z(x^2+y... ...\ \varrho z^2\sin\varphi \\ \varrho^2 z\\ \end{array}\right) \end{displaymath}

von innen nach außen durch den Mantel eines Zylinders mit Abstand $ a$ zur $ z$-Achse und $ z_{\rm min}=0$, $ z_{\rm max}=b$ berechnet werden.

Man erhält

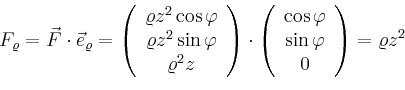
\begin{displaymath} F_\varrho=\vec{F}\cdot \vec{e}_\varrho= \left( \begin{array}... ...s\varphi\\ \sin\varphi\\ 0\\ \end{array}\right) = \varrho z^2 \end{displaymath}

und somit für den Fluss

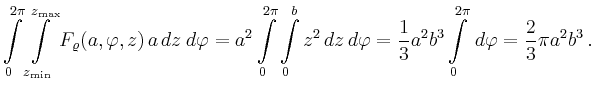
$\displaystyle \int\limits_0^{2\pi}\int\limits_{z_{\min}}^{z_{\max}} F_\varrho(a... ...= \frac{1}{3}a^2b^3 \int\limits_0^{2\pi} \,d\varphi = \frac{2}{3}\pi a^2b^3\,. $

Der Fluss des Vektorfeldes

$\displaystyle \vec{F}=\varrho \vec{e}_\varrho +z\vec{e}_z $

nach außen durch einen Zylindermantel, der durch die Kardioide $ \varrho(\varphi)=1-\cos \varphi$ im Bereich $ z\in[0,a]$ erzeugt wird, ist

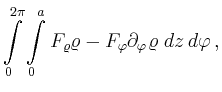
$\displaystyle \int\limits_0^{2\pi}\int\limits_{0}^{a} F_\varrho \varrho- F_\varphi \partial_\varphi \varrho \,\,dz\,d\varphi \,, $

und mit $ F_\varrho=\varrho \,,\, F_\varphi =0$ ergibt sich

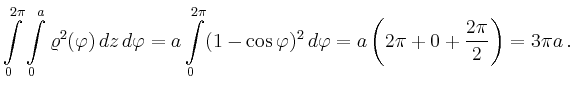
$\displaystyle \int\limits_0^{2\pi}\int\limits_{0}^{a} \varrho^2(\varphi) \,dz\,... ...i} (1-\cos \varphi)^2 \,d\varphi=a\left(2\pi+0+\frac{2\pi}{2}\right)=3\pi a\,. $

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 9.10.2013