Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Vektoranalysis - Integration - Flächenintegrale

Fluss durch eine Sphäre

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Der Fluss eines Vektorfeldes

$\displaystyle \vec{F}(r,\vartheta,\varphi) = F_r \vec{e}_r + F_\vartheta \vec{e}_\vartheta + F_\varphi \vec{e}_\varphi $

von innen nach außen durch eine Sphäre mit Abstand $ r=a$ zum Ursprung ist

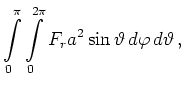
$\displaystyle \int\limits_0^\pi\int\limits_0^{2\pi} F_r a^2\sin\vartheta\,d\varphi\,d\vartheta \,, $

d.h. nur die radiale Komponente des Feldes liefert einen Beitrag.

Insbesondere ist der Fluss für ein radiales Feld $ \vec{F} = f(r)\,\vec{e}_r$ gleich $ 4\pi a^2 f(a)$.

Es soll der Fluss des Vektorfeldes

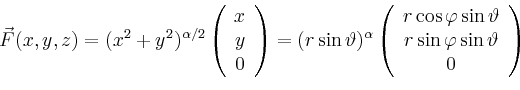
\begin{displaymath} \vec{F}(x,y,z)=(x^2+y^2)^{\alpha/2}\left( \begin{array}{c} x... ...rtheta\\ r\sin\varphi\sin\vartheta\\ 0\\ \end{array}\right) \end{displaymath}

von innen nach außen durch die Sphäre mit Radius $ a$ berechnet werden.

Man erhält

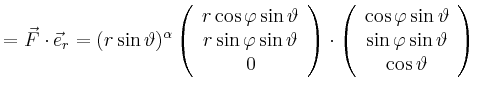$\displaystyle F_r (r,\vartheta,\varphi)$ $\displaystyle =\vec{F} \cdot \vec{e}_r= (r\sin\vartheta)^\alpha\left( \begin{ar... ...hi\sin\vartheta\\ \sin\varphi\sin\vartheta\\ \cos\vartheta\\ \end{array}\right)$    
  $\displaystyle =(r\sin\vartheta)^\alpha r\sin^2\vartheta$    

und somit für den Fluss

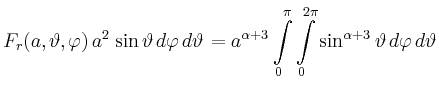$\displaystyle \int\limits_0^\pi\int\limits_0^{2\pi}$ $\displaystyle F_r(a,\vartheta,\varphi)\, a^2\sin\vartheta\,d\varphi\,d\vartheta... ...limits_0^\pi\int\limits_0^{2\pi} \sin^{\alpha+3}\vartheta\,d\varphi\,d\vartheta$    
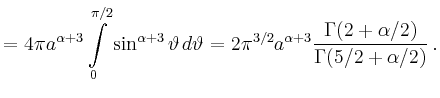  $\displaystyle = 4\pi a^{\alpha+3}\int\limits_0^{\pi/2}\sin^{\alpha+3}\vartheta\... ...heta = 2\pi^{3/2}a^{\alpha+3}\frac{\Gamma(2+\alpha/2)}{\Gamma(5/2+\alpha/2)}\,.$    

Es soll der Fluss der senkrechten Strömung

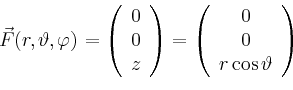
\begin{displaymath} \vec{F}(r,\vartheta,\varphi)= \left( \begin{array}{c} 0\\ 0\... ...\begin{array}{c} 0\\ 0\\ r\cos \vartheta\\ \end{array}\right) \end{displaymath}

von unten nach oben durch die Halbkugelschale

$\displaystyle r=a,\quad 0\leq\varphi\leq2\pi,\quad 0\leq\vartheta\leq\pi/2 $

berechnet werden.

Man erhält

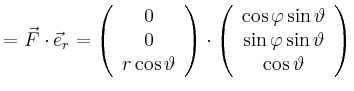$\displaystyle F_r(r,\vartheta,\varphi)$ $\displaystyle =\vec{F} \cdot \vec{e}_r = \left( \begin{array}{c} 0\\ 0\\ r\cos\... ...hi\sin\vartheta\\ \sin\varphi\sin\vartheta\\ \cos\vartheta\\ \end{array}\right)$    
  $\displaystyle =r\cos^2\vartheta$    

und somit für den Fluss

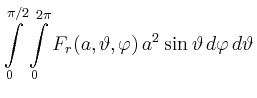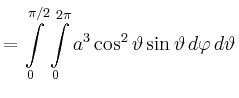$\displaystyle \int\limits_0^{\pi/2}\int\limits_0^{2\pi} F_r(a,\vartheta,\varphi)\,a^2\sin\vartheta\,d\varphi\,d\vartheta$ $\displaystyle = \int\limits_0^{\pi/2}\int\limits_0^{2\pi} a^3\cos^2\vartheta \sin\vartheta \,d\varphi\,d\vartheta$    
  $\displaystyle = 2\pi a^3\left[\frac{-\cos^3\vartheta}{3}\right]_{\vartheta=0}^{\pi/2}$    
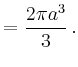  $\displaystyle = \frac{2\pi a^3}{3}\,.$    

Die Projektion eines axialsymmetrischen Feldes

$\displaystyle \vec{F}(\varrho,z) = F_\varrho\vec{e}_\varrho+F_\varphi\vec{e}_\varphi+F_z\vec{e}_z $

auf die Einheitsnormale der Kugeloberfläche mit Radius $ a$,

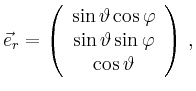
$\displaystyle \vec{e}_r = \left(\begin{array}{c} \sin \vartheta \cos \varphi\\ \sin \vartheta \sin \varphi\\ \cos \vartheta \end{array}\right)\,, $

ergibt mit

$\displaystyle \vec{e}_\varrho \cdot \vec{e}_r = \sin \vartheta\,,\quad \vec{e}_\varphi \cdot \vec{e}_r = 0\,,\quad \vec{e}_z \cdot \vec{e}_r = \cos \vartheta $

die radiale Komponente $ F_r = F_\varrho\sin\vartheta + F_z\cos\vartheta$ und damit den Fluss

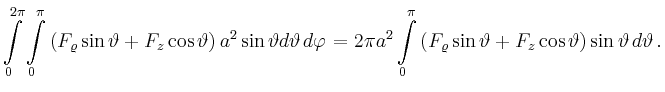
$\displaystyle \int\limits_0^{2\pi} \int\limits_0^\pi \left(F_\varrho\sin\varthe... ...rrho\sin\vartheta + F_z \cos \vartheta \right) \sin \vartheta\, d\vartheta\,. $

Speziell gilt für $ F_\varrho = \varrho^{2s}\,,\,F_z=c$

$\displaystyle F_r = F_\varrho\sin\vartheta + F_z \cos \vartheta = a^{2s} \sin^{2s+1} \vartheta + c\cos \vartheta\,. $

Der zweite Summand verschwindet bei der Integration, so dass sich als Fluss insgesamt

$\displaystyle 2\pi a^2 \int\limits_0^\pi a^{2s} \sin^{2s+2} \vartheta\, d\varth... ..., \pi =2\pi^2 \left(\frac{a}{2}\right)^{2(s+1)} \frac{(2(s+1))!}{ ((s+1)!)^2} $

ergibt.
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 9.10.2013