Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Vektoranalysis - Potentialtheorie - Skalares Potential

Existenz eines Potentials

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Für ein stetiges Vektorfeld $ \vec{F}$ auf einem zusammenhängenden Gebiet $ D$ existiert ein Potential $ U$ genau dann, wenn das Arbeitsintegral wegunabhängig ist. In diesem Fall ist

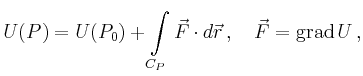
$\displaystyle U(P) = U(P_0)+ \int\limits_{C_P} \vec{F} \cdot d\vec{r}\,, \quad \vec{F} = \operatorname{grad} U \,, $

wobei $ {C_P}: t\mapsto \vec{r}(t)$ ein beliebiger in $ D$ verlaufender Weg ist, der einen fest gewählten Punkt $ P_0\in D$ mit $ P$ verbindet. Insbesondere ist $ U$ bis auf eine Konstante (den Wert $ U(P_0)$) eindeutig bestimmt.

Ist $ \vec{F}$ stetig differenzierbar auf einer offenen Menge $ D$ ist

$\displaystyle \operatorname{rot} \vec{F} =0 $

notwendig für die Existenz eines Potentials. Ist $ D$ einfach zusammenhängend, so ist die Wirbelfreiheit ebenfalls hinreichend.

Die Wegunabhängigkeit ist notwendig, da

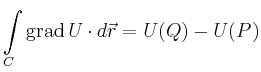
$\displaystyle \int\limits_{C} \operatorname{grad}U\cdot d\vec{r} = U(Q)-U(P) $

für jeden die Punkte $ P$ und $ Q$ verbindenden Weg $ C$ gilt.

Dass die Wegunabhängigkeit hinreichend ist, ergibt sich aus folgender Überlegung:

Da $ D$ offen ist, gibt es zu einem Punkt $ P$ einen Wert $ h>0$, so dass für $ \vec{q}=\vec{p}+h\vec{e}_i$ die gesamte Strecke $ S=\overline{PQ}$ in $ D$ enthalten ist.

\includegraphics[width=.5\linewidth]{e_potential_existenz_bild}

Aufgrund der Wegunabhängigkeit des Arbeitsintegrals kann man nun für den Wert $ U(Q)$ den Weg $ C_P$ zu $ P$ um die Strecke $ S$ ergänzen. Dann ergibt sich für die Potentialdifferenz

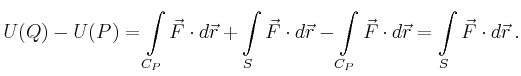
$\displaystyle U(Q)-U(P) = \int\limits_{C_P} \vec{F}\cdot d\vec{r} + \int\limit... ...nt\limits_{C_P} \vec{F}\cdot d\vec{r} =\int\limits_S \vec{F} \cdot d\vec{r}\,. $

Mit der Parametrisierung

$\displaystyle S: \vec{r}(t) = \vec{p}+t\vec{e}_i\,,\quad t \in [0,h]\,, $

ist

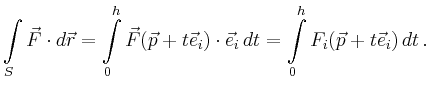
$\displaystyle \int\limits_S \vec{F} \cdot d\vec{r} = \int\limits_0^h \vec{F}(\v... ...ec{e}_i)\cdot \vec{e}_i\, dt = \int\limits_0^h F_i(\vec{p}+t\vec{e}_i)\, dt\,. $

Der Mittelwertsatz der Integralrechnung liefert nun

$\displaystyle \int\limits_0^h F_i(\vec{p}+t\vec{e}_i) dt = hF_i(\vec{p}+\tau \vec{e}_i)\,,\quad \tau \in[0,h]\,. $

Für die $ i$-te Komponente des Gradienten folgt also

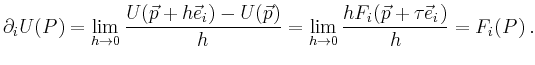
$\displaystyle \partial_i U (P)= \lim\limits_{h\to 0} \frac{U(\vec{p}+h\vec{e}_i... ...)}{h} =\lim\limits_{h\to 0} \frac{hF_i(\vec{p}+\tau \vec{e}_i)}{h} = F_i(P)\,. $

Somit ist $ U$ tatsächlich ein Potential für $ \vec{F}$.

Für stetig differenzierbare Vektorfelder folgt die Notwendigkeit der Wirbelfreiheit unmittelbar aus der Vertauschbarkeit der partiellen Ableitungen. Ist $ \vec{F}=\operatorname{grad}U$, so folgt

$\displaystyle \partial_iF_j-\partial_jF_i= \partial_i\partial_j U - \partial_j\partial_i U = 0\,. $

Ist $ D$ einfach zusammenhängend, so berandet jede geschlossene Kurve $ C$ eine Fläche $ S$ in $ D$. Der Satz von Stokes,

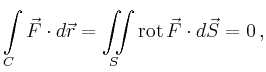
$\displaystyle \int\limits_C \vec{F}\cdot d\vec{r} = \iint\limits_S \operatorname{rot} \vec{F}\cdot d\vec{S} =0\,, $

impliziert damit die Wegunabhängigkeit.
Zu bestimmen ist das Potential des ebenen Vektorfelds

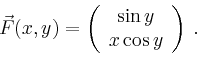
\begin{displaymath} \vec{F}(x,y)=\left( \begin{array}{c} \sin y\\ x\cos y \\ \end{array}\right)\,. \end{displaymath}

Als festen Punkt $ P_0$ wählen wir den Ursprung und als Kurve von $ O$ nach $ P$ die direkte Verbindung

\begin{displaymath} C_P:\quad \vec{r}(t)=\left( \begin{array}{c} p_1t\\ p_2t\\ \end{array}\right),\quad t\in[0,1]\,. \end{displaymath}

Für die Potentialfunktion $ U$ erhalten wir dann

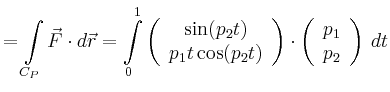$\displaystyle U(P)$ $\displaystyle = \int\limits_{C_P} \vec{F}\cdot d\vec{r} = \int\limits_0^1 \left... ...rray}\right) \cdot \left( \begin{array}{c} p_1 \\ p_2\\ \end{array}\right) \,dt$    
  $\displaystyle = \int\limits_0^1 p_1\sin(p_2t) +p_1p_2t\cos(p_2t)\,dt = \left[p_1t\sin(p_2t)\right]_0^1 = p_1\sin p_2\,.$    

Für ein lineares Feld

$\displaystyle \vec{F}=A\vec{r}\,,\quad A=\left(a_{j,k}\right)\,, $

ist

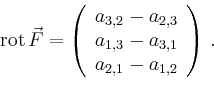
\begin{displaymath} \operatorname{rot}\vec{F} = \left( \begin{array}{c} a_{3,2... ...\ a_{1,3}-a_{3,1}\\ a_{2,1}-a_{1,2}\\ \end{array}\right)\,. \end{displaymath}

Ein Potential $ U$ existiert also genau dann, wenn $ A$ symmetrisch ist. In diesem Fall ist

$\displaystyle U=\frac{1}{2} \vec{r}\,^\mathrm{t} A \vec{r} \,. $

Differenziert man das Skalarfeld

$\displaystyle U=\arctan(y/x) = \varphi\,, $

so erhält man

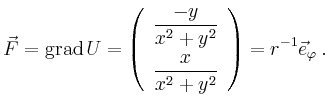
$\displaystyle \vec{F} = \operatorname{grad}U = \left(\begin{array}{c} \displays... ...\displaystyle \frac{x}{x^2+y^2}\end{array}\right) = r^{-1} \vec{e}_\varphi\,. $

Bis auf die Singularität im Ursprung erfüllt dieses Feld die Integrabilitätsbedingung

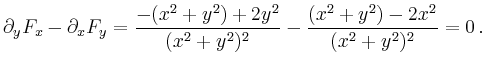
$\displaystyle \partial_yF_x-\partial_xF_y = \frac{-(x^2+y^2)+2y^2}{(x^2+y^2)^2} - \frac{(x^2+y^2)-2x^2}{(x^2+y^2)^2} = 0\,. $

Dennoch ist das Arbeitsintegral auf einem Kreis $ K$ mit Radius $ a$ um den Ursprung nicht null:

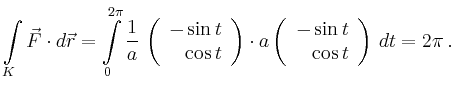
$\displaystyle \int\limits_K \vec{F}\cdot d\vec{r} = \int\limits_0^{2\pi} \frac{... ...ot a \left(\begin{array}{r} -\sin t \\ \cos t \end{array}\right)\,dt = 2\pi\,. $

Obwohl $ \vec{F} = \operatorname{grad}U$ gilt, existiert kein (global definiertes) Potential. Dies liegt an der Singularität im Ursprung. Das Gebiet, auf dem die Integrabilitätsbedingung erfüllt ist, ist nicht einfach zusammenhängend. Die Problematik wird auch klar, wenn man berücksichtigt, dass die Funktion $ U=\varphi$ auf einem Kreisring um den Ursprung nicht stetig definiert werden kann.

Natürlich existiert ein Potential (nämlich $ U=\varphi$) auf jeder einfach zusammenhängenden Menge, die den Ursprung nicht enthält.

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 9.10.2013