Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Fourier-Analysis - Diskrete Fourier-Transformation - Anwendungen

Fourier-Filter

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Die trigonometrische Interpolation in Verbindung mit der diskreten Fourier-Transformation kann zum Ausblenden hochfrequenter Störungen in Signalen verwendet werden.

Man bildet zu den Daten

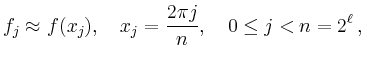
$\displaystyle f_j \approx f(x_j),\quad x_j = \frac{2\pi j}{n},\quad 0\le j<n=2^\ell \,, $

zunächst mit Hilfe der schnellen Fourier-Transformation das trigonometrische Interpolationspolynom

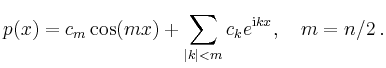
$\displaystyle p(x) = c_m \cos(mx) + \sum_{\vert k\vert < m} c_k e^{\mathrm{i}kx}, \quad m=n/2 \,. $

Dann wählt man eine Bandbreite $ M$ und setzt alle Koeffizienten $ c_k$ mit $ \vert k\vert>M$ null. Mit diesem Tiefpass werden für hinreichend kleines $ M$ im Allgemeinen Störungen unterdrückt.

\includegraphics[width=.4\linewidth]{sprachsig_org}                 \includegraphics[width=.42\linewidth]{sprachsig_org_500amplituden}

\includegraphics[width=.4\linewidth]{sprachsig_gedaempft}                 \includegraphics[width=.42\linewidth]{sprachsig_gedaempft_500amplituden}

\includegraphics[width=.4\linewidth]{sprachsig_stark_gedaempft}                 \includegraphics[width=.42\linewidth]{sprachsig_stark_gedaempft_500amplituden}

Die Abbildung zeigt oben links ein Sprachsignal $ f(x)$ und rechts die ersten 500 der 40000 Amplituden $ \vert\mathrm{Re}(c_k)\vert$. Die darunter abgebildeten Approximationen illustrieren den Glättungseffekt für die Bandbreiten $ M=400$ und $ M=100$. Man sieht auch, dass eine zu kleine Bandbreite zu einem unerwünschten Genauigkeitsverlust führen kann.

Bei der Implementierung ist zu beachten, dass die inverse diskrete Fourier-Transformation der Daten

$\displaystyle f_0,\ldots,f_{n-1} $

das trigonometrische Polynom

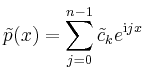
$\displaystyle \tilde p(x) = \sum_{j=0}^{n-1} \tilde c_k e^{\mathrm{i}jx} $

berechnet. Auf dem Auswertungsgitter

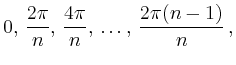
$\displaystyle 0,\,\frac{2\pi}{n},\,\frac{4\pi}{n},\, \ldots,\, \frac{2\pi(n-1)}{n} \,, $

können jedoch die Exponentialfunktionen

$\displaystyle e^{\mathrm{i}jx},\quad e^{\mathrm{i}(j-n)x} $

nicht unterschieden werden, d.h. es gilt

$\displaystyle (c_{-m+1},\ldots,c_m) = (\tilde c_{m+1},\ldots,\tilde c_{n-1}, \tilde c_0,\tilde{c}_1,\ldots,\tilde c_m) \,. $

Damit lässt sich ein Fourier-Filter mit dem folgenden Programmsegment realisieren:

         IFFT: $ f_j\to\tilde c_k$
  $ \tilde c_{M+1},\ldots,\tilde c_{n-1-M}$ auf null setzen
  FFT: $ \tilde c_k\to p(x_j)$

Werden anstatt der oberen die unteren Koeffizienten auf null gesetzt, ergibt das Verfahren einen Hochpass.

(Autor: Patrick Wagner )
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 13.11.2013