Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Fourier-Analysis - Diskrete Fourier-Transformation - Anwendungen

Fourier-Transformation zyklischer Gleichungssysteme

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Eine zyklische Matrix

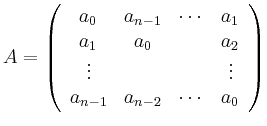
$\displaystyle A = \left(\begin{array}{cccc} a_0 & a_{n-1} & \cdots & a_1 \\ a_... ... \\ \vdots &&& \vdots \\ a_{n-1} & a_{n-2} & \cdots & a_0 \end{array}\right) $

besitzt die Eigenwerte

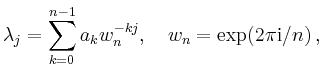
$\displaystyle \lambda_j = \sum_{k=0}^{n-1} a_k w_n^{-kj},\quad w_n = \exp(2\pi\mathrm{i}/n) \,, $

und kann durch die Fourier-Matrix diagonalisiert werden:

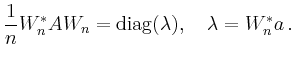
$\displaystyle \frac{1}{n} W_n^\ast A W_n = \operatorname{diag}(\lambda), \quad \lambda = W_n^\ast a \,. $

Folglich lässt sich die Lösung eines zyklischen Gleichungssystems $ Ax = b$ in der Form

$\displaystyle x = W_n \operatorname{diag}(\lambda)^{-1} (W_n^\ast b/n) $

berechnen.

Für $ n=2^\ell$ ist die schnelle Fourier-Transformation anwendbar, und man erhält den folgenden Lösungsalgorithmus:

         $ c = \operatorname{IFFT}(b)$
  $ \lambda = n\,\operatorname{IFFT}(a)$
  $ y_j = c_j /\lambda_j$,     $ j=0,\ldots,n-1$
  $ x = \operatorname{FFT}(y)\,.$

Um zu zeigen, dass die Fourier-Matrix die zyklische Matrix diagonalisiert, wird die Beziehung $ AW_n = W_n \Lambda$ mit $ \Lambda =\operatorname{diag}(\lambda)$ geprüft.

Der $ (j+1)$-ste Eintrag in der $ (\ell+1)$-sten Spalte des Matrixprodukts $ AW_n$ ist

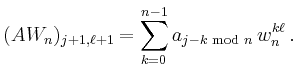
$\displaystyle (AW_n)_{j+1,\ell+1} = \sum_{k=0}^{n-1} a_{j-k\,\operatorname{mod}\,n}\,w_n^{k\ell}\,. $

Die Substitution $ k=j-k^\prime$ führt auf

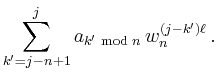
$\displaystyle \sum_{k^\prime=j-n+1}^{j} a_{k^\prime\,\operatorname{mod}\,n}\,w_n^{(j-k^\prime)\ell}\,. $

Aus dieser Summe kann nun der gemeinsame Faktor $ w_n^{j\ell}$ ausgeklammert werden. Da $ w_n^n=1$, kann auch $ k^\prime$ im Exponenten von $ w_n$ Modulo $ n$ betrachtet werden, bzw. die Summe umsortiert und über die möglichen Reste gebildet werden. Dies liefert

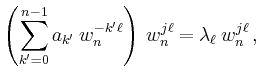
$\displaystyle \left( \sum_{k^\prime=0}^{n-1} a_{k^\prime}\,w_n^{-k^\prime\ell} \right)\, w_n^{j\ell} = \lambda_\ell\,w_n^{j\ell}\,, $

die $ (\ell+1)$-ste Spalte des Produkts ist also das $ \lambda_\ell$-fache der entsprechenden Spalte der Fourier-Matrix: $ AW_n = W_n \Lambda$.

Multipliziert man das Gleichungssystems $ Ax = b$ mit $ W_n^*/n$ und substitutiert $ x = W_n y$ erhält man

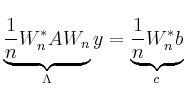
$\displaystyle \underbrace{\frac{1}{n} W_n^* A W_n}_{\Lambda} y = \underbrace{\frac{1}{n} W_n^* b}_{c} $

mit der Lösung $ y = \Lambda^{-1} c$.

Als Beispiel soll das lineare Gleichungssystem $ Ax=b$ mit

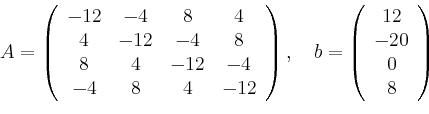
\begin{displaymath} A=\left( \begin{array}{cccc} -12 & -4 & 8 & 4\\ 4 & -12 & -... ...\left( \begin{array}{c} 12\\ -20\\ 0\\ 8\\ \end{array}\right) \end{displaymath}

gelöst werden.

Mitt $ n=4$, $ a=(-12,4,8,-4)^{\operatorname t}$ ist

$\displaystyle c$ $\displaystyle = \operatorname{IFFT}(b) = (0,3+7\mathrm{i},6,3-7\mathrm{i})^{\operatorname t}$    
$\displaystyle \lambda$ $\displaystyle = 4 \cdot \operatorname{IFFT}(a) = (-4,-20-8\mathrm{i},-4,-20+8\mathrm{i})^{\operatorname t}\,.$    

Nach Bilden von $ y_j = c_j /\lambda_j$ folgt somit


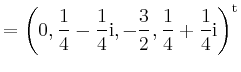$\displaystyle y$ $\displaystyle = \left(0, \frac{1}{4}-\frac{1}{4}\mathrm{i}, -\frac{3}{2}, \frac{1}{4}+\frac{1}{4}\mathrm{i}\right)^{\operatorname t}$    
$\displaystyle x$ $\displaystyle = \operatorname{FFT}(y) = (-2,2,-1,1)^{\operatorname t}\,.$    

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 13.11.2013