Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Fourier-Analysis - Fourier-Transformation - Definition und Eigenschaften

Fourier-Transformation

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Existiert zu einer Funktion $ f$ das Parameterintegral

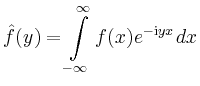
$\displaystyle \hat{f}(y) = \int\limits_{-\infty}^\infty f(x)e^{-\mathrm{i}yx}\,dx $

für alle $ y\in\mathbb{R}$, so heißt $ f$ Fourier-transformierbar und die Funktion $ \hat{f}$ Fourier-Transformierte von $ f$. Man schreibt

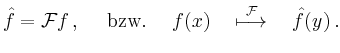
$\displaystyle \hat{f} = {\cal F} f \,,\quad \textrm{ bzw. } \quad f(x) \quad\overset{\cal F }{\longmapsto}\quad \hat{f}(y)\,. $

Entsprechend ist die inverse Fourier-Transformation $ {\cal F}^{-1}$ durch

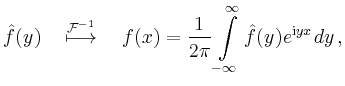
$\displaystyle \hat{f}(y)\quad \overset{{\cal F}^{-1}}{\longmapsto} \quad f(x) = \frac{1}{2\pi} \int\limits_{-\infty}^\infty \hat{f}(y)e^{\mathrm{i}yx}\,dy\,, $

definiert und es gilt

$\displaystyle f={\cal F}^{-1}{\cal F}f $

für absolut integrierbare, stetig differenzierbare Funktionen $ f$.

Die Fourier-Transformation und die inverse Fourier-Transformation sind linear. Sie unterscheiden sich nur unwesentlich. Es ist

$\displaystyle {\cal F} \bar{f} = 2\pi \overline{{\cal F}^{-1} f}\,. $

Man kann die inverse Fourier-Transformation als kontinuierliche Entwicklung nach den Exponentialfunktionen $ e_k(x)=e^{\mathrm{i}kx}$ interpretieren. Nimmt man an, dass $ f$ außerhalb eines Intervalles $ [-h,h]$ null ist, so gilt

$\displaystyle f(x) = \sum_{k=-\infty}^\infty \left[ \frac{1}{2h} \int\limits_{-h}^h f(t) \overline{e_k(t \pi/h)}\,dt \right] e_k(x \pi/h) $

für $ x\in[-h,h]$. Nach Definition von $ \hat{f}$ gilt somit

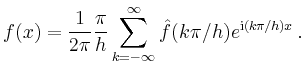
$\displaystyle f(x) = \frac{1}{2\pi}\frac{\pi}{h} \sum_{k=-\infty}^\infty \hat{f}(k\pi/h) e^{\mathrm{i}(k\pi/h)x} \,. $

Diese Riemann-Summe ist eine Approximation der inversen Fourier-Transformation und konvergiert bei hinreichend glattem $ \hat{f}$ für $ \Delta y=\pi/h\to 0$.

Aufgrund der obigen Überlegungen kann die Fourier-Transformation in gewissem Sinn als Grenzfall der Fourier-Reihe interpretiert werden. Ein rigoroser Beweis der Umkehrformel ist allerdings wesentlich aufwendiger.

Gesucht wird die Fourier-Transformation der Impuls-Funktion zum Standard-Intervall $ [-1/2,1/2]$

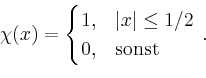
\begin{displaymath} \chi(x)= \begin{cases} 1,& \vert x\vert\leq 1/2\\ 0,&\text{sonst} \end{cases}\,. \end{displaymath}

Man erhält

$\displaystyle \hat{\chi}(y)= \int\limits_{-1/2}^{1/2} e^{-\mathrm{i}yx}\,dx = \... ...m{i}y}\right]_{-1/2}^{1/2} = \frac{\sin(y/2)}{y/2}=\operatorname{sinc}(y/2)\,. $

Gesucht wird die Fourier-Transformation der Funktion

$\displaystyle f(x)=e^{-\vert x\vert}\,. $

Mit der Formel von Euler-Moivre folgt e$ ^{-\text{i}xy} =\cos (xy)-\text{i}\sin(xy)$. Da $ f$ gerade ist, ist $ \int_{-\infty}^\infty f(x) \sin(xy) dx =0 $ und

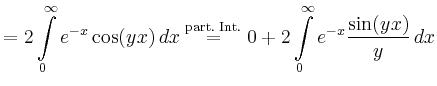$\displaystyle \hat{f}(y)$ $\displaystyle = 2\int\limits_0^\infty e^{-x}\cos(yx)\,dx \overset{\text{part. Int.}}{=} 0+2\int\limits_0^\infty e^{-x}\frac{\sin(yx)}{y}\,dx$    
  $\displaystyle \overset{\text{part. Int.}}{=} 2\left[e^{-x}\left(-\frac{\cos(yx)... ...}\right)\right]_0^\infty - 2\int\limits_0^\infty e^{-x}\frac{\cos(yx)}{y^2}\,dx$    
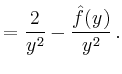  $\displaystyle = \frac{2}{y^2} - \frac{\hat{f}(y)}{y^2}\,.$    

Aufgelöst ergibt sich


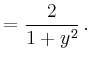$\displaystyle \hat{f}(y)$ $\displaystyle = \frac{2}{1+y^2}\,.$    

Die Gauß-Funktion ist eine Eigenfunktion der Fourier-Transformation:

$\displaystyle f(x) = \exp(-x^2/2) \quad \Leftrightarrow \quad \hat{f}(y) = \sqrt{2\pi}\exp(-y^2/2) \,. $

Zum Beweis schreibt man das Fourier-Integral in der Form

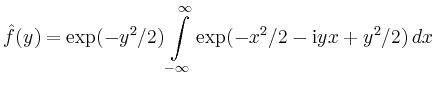
$\displaystyle \hat{f}(y) = \exp(-y^2/2) \int\limits_{-\infty}^\infty \exp(-x^2/2 - \mathrm{i}yx + y^2/2)\,dx $

und setzt

$\displaystyle -z^2/2 = -(x+\mathrm{i}y)^2/2 \,. $

Mit Mitteln der komplexen Analysis lässt sich nun zeigen, dass der Integrationsweg verschoben werden kann: $ z\leftarrow z-\mathrm{i}y$. Damit kann die Berechnung der Fourier-Transformation auf das bekannte Integral

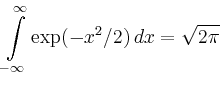
$\displaystyle \int\limits_{-\infty}^\infty \exp(-x^2/2)\,dx = \sqrt{2\pi} $

zurückgeführt werden.
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 13.11.2013