Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Fourier-Analysis - Fourier-Reihen - Komplexe Fourier-Reihen

Zusammenhang komplexer und reeller Fourier-Reihen

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Die komplexe Fourier-Reihe

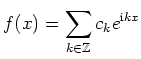
$\displaystyle f(x) =\sum_{k\in\mathbb{Z}} c_k e^{\mathrm{i}kx} $

lässt sich auch in Sinus-Kosinus-Form darstellen:

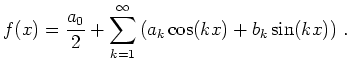
$\displaystyle f(x) =\frac{a_0}{2} + \sum_{k=1}^\infty \left( a_k\cos(kx)+b_k\sin(kx)\right)\,. $

Für die Koeffizienten gelten dabei die Umrechnungsformeln

$\displaystyle a_0=2c_0,\quad a_k=c_k+c_{-k},\quad b_k=\mathrm{i}(c_k-c_{-k})\,,\quad(k\geq 1)\,, $

bzw.

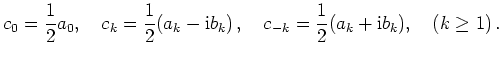
$\displaystyle c_0=\frac{1}{2}a_0,\quad c_k=\frac{1}{2}(a_k -\mathrm{i}b_k)\,,\quad c_{-k}=\frac{1}{2}(a_k +\mathrm{i}b_k),\quad(k\geq 1)\,. $

Die Fourier-Reihe ist genau dann reell, wenn $ c_{-k}=\overline{c_k}$ gilt.
Aus der Formel von Euler-Moivre

$\displaystyle \mathrm{e}^{\mathrm{i} t} = \cos t + \mathrm{i} \sin t $

folgt

$\displaystyle c_k \mathrm{e}^{\mathrm{i}kx} +c_{-k} \mathrm{e}^{-\mathrm{i}kx} ... ...s(kx) + \mathrm{i}c_k \sin(kx) +c_{-k}\cos(kx) - \mathrm{i}c_{-k} \sin(kx)\, . $

Wegen der Symmetrie des Kosinus bzw. der Antisymmetrie des Sinus ist also

$\displaystyle a_k = c_k +c_{-k}\,,\quad b_k = \mathrm{i}(c_k -c_{-k})\, . $

Für reelle Koeffizienten gilt

$\displaystyle a_k = \bar{a}_k \land b_k = \bar{b}_k\,, $

d.h.

$\displaystyle c_k +c_{-k} = \bar{c}_k + \bar{c}_{-k} \land c_k - c_{-k} = -\bar{c}_k + \bar{c}_{-k}\,, $

und Addition der Gleichungen ergibt $ c_k = \bar{c}_{-k}$
Gesucht wird die reelle und die komplexe Fourier-Reihe der Funktion

$\displaystyle f(x) = \sin^4 x + \cos^3 x\,. $

\includegraphics[width=.8\linewidth]{b_komplex_reell}

Die Funktion ist gerade und lässt sich durch Kosinus-Funktionen ausdrücken:

$\displaystyle f(x) = (1-\cos ^2x)^2 + \cos^3 x = 1-2\cos^2 x +\cos ^3x +\cos^4 x $

Aus den Additionstheoremen

$\displaystyle \cos (\alpha+\beta)$ $\displaystyle =$ $\displaystyle \cos \alpha \cos \beta -\sin \alpha \sin \beta$  
$\displaystyle \sin (\alpha+\beta)$ $\displaystyle =$ $\displaystyle \sin \alpha \cos \beta +\cos \alpha \sin \beta$  

erhält man
$\displaystyle \cos (2x)$ $\displaystyle =$ $\displaystyle \cos^2x-\sin^2x = 2\cos^2 x -1$  
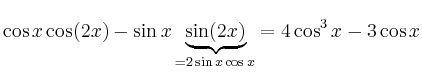$\displaystyle \cos (3x)$ $\displaystyle =$ $\displaystyle \cos x \cos(2x) -\sin x\underbrace{\sin(2x)}_{=2\sin x \cos x} = 4\cos^3 x -3\cos x$  
$\displaystyle \cos (4x)$ $\displaystyle =$ $\displaystyle 2\left(\cos(2x)\right)^2-1 = 8 \cos^4 x -8 \cos ^2 x +1$  

und sukzessives Auflösen ergibt
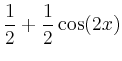$\displaystyle \cos^2 x$ $\displaystyle =$ $\displaystyle \frac12 +\frac12 \cos(2x)$  
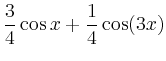$\displaystyle \cos^3 x$ $\displaystyle =$ $\displaystyle \frac34\cos x +\frac14 \cos(3x)$  
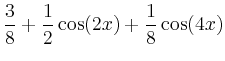$\displaystyle \cos^4 x$ $\displaystyle =$ $\displaystyle \frac38+\frac12\cos(2x) +\frac18 \cos(4x)$  

Einsetzen in $ f$ liefert
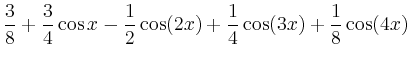$\displaystyle f(x)$ $\displaystyle =$ $\displaystyle \frac{3}{8} + \frac{3}{4}\cos x - \frac{1}{2}\cos(2x) + \frac{1}{4}\cos(3x) + \frac{1}{8}\cos(4x)$  

als reelle Fourier-Reihe von $ f$ mit den von null verschiedenen Koeffizienten

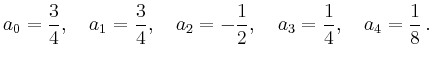
$\displaystyle a_0=\frac{3}{4},\quad a_1=\frac{3}{4},\quad a_2=-\frac{1}{2},\quad a_3=\frac{1}{4},\quad a_4=\frac{1}{8}\,. $

Mit den Umrechnungsformeln ergeben sich somit für die von null verschiedenen Koeffizienten der komplexen Fourier-Reihe

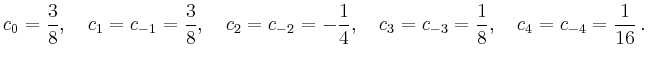
$\displaystyle c_0=\frac{3}{8},\quad c_1=c_{-1}=\frac{3}{8},\quad c_2=c_{-2}=-\frac{1}{4},\quad c_3=c_{-3}=\frac{1}{8},\quad c_4=c_{-4}=\frac{1}{16}\,. $

Die komplexe Fourier-Reihe von $ f$ lautet also

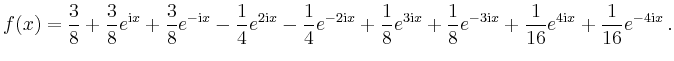
$\displaystyle f(x) =\frac{3}{8} +\frac{3}{8}e^{\mathrm{i}x}+\frac{3}{8}e^{-\mat... ...{-3\mathrm{i}x} +\frac{1}{16}e^{4\mathrm{i}x}+\frac{1}{16}e^{-4\mathrm{i}x}\,. $

Alternativ kann man die komplexe Entwicklung auch mit Hilfe der Formeln von Euler-Moivre,

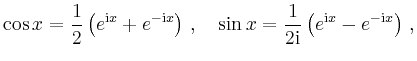
$\displaystyle \cos x = \frac{1}{2}\left(e^{\mathrm{i}x}+e^{-\mathrm{i}x}\right)... ...\sin x = \frac{1}{2\mathrm{i}}\left(e^{\mathrm{i}x}-e^{-\mathrm{i}x}\right)\,, $

herleiten.
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 13.11.2013