Mathematik-Online-Kurs: Repetitorium HM III-Wahrscheinlichkeitsrechnung und Statistik-Zufallsvariable und Erwartungswert

	[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
	Mathematik-Online-Kurs: Repetitorium HM III - Wahrscheinlichkeitsrechnung und Statistik
	Zufallsvariable und Erwartungswert

[vorangehende Seite] [nachfolgende Seite]

[Gesamtverzeichnis][Seitenübersicht]

Zufallsvariablen sind von den Elementarereignissen abhängige Meßgrößen, über die wahrscheinlichkeitstheoretische Aussagen getroffen werden sollen. So z.B. kann man sich fragen, welche Meßgröße im Mittel erwartet werden kann.

Eine Zufallsvariable $\mbox{$X$}$ ist eine Funktion $\mbox{$X:\Omega\longrightarrow \mathbb{R}$}$ , für die $\mbox{$\{\omega\in\Omega\; \vert\; X(\omega)\leq t\}$}$ ein meßbares Ereignis ist für alle $\mbox{$t\in\mathbb{R}$}$ . Die Wahrscheinlichkeit $\mbox{$F(t) := P(\{\omega\in\Omega\; \vert\; X(\omega)\leq t\})$}$ dieses Ereignisses in Abhängigkeit von $\mbox{$t\in\mathbb{R}$}$ heißt auch Verteilungsfunktion von $\mbox{$X$}$ .

Für $\mbox{$t\in\mathbb{R}$}$ schreiben wir auch $\mbox{$(X = t) :=\{\omega\in\Omega\; \vert\; X(\omega) = t\}$}$ , $\mbox{$(X \leq t) := \{\omega\in\Omega\; \vert\; X(\omega) \leq t\}$}$ etc.

Sei $\mbox{$I$}$ eine Indexmenge. Die Zufallsvariablen $\mbox{$X_i$}$ für $\mbox{$i\in I$}$ heißen unabhängig, falls die Ereignisse $\mbox{$(X_{i_1}\leq t_1),\dots, (X_{i_n}\leq t_n)$}$ unabhängig sind für alle endlichen Indextupel $\mbox{$(i_1,\dots i_n)$}$ und je alle $\mbox{$t_j\in [-\infty,+\infty]$}$ , $\mbox{$1\leq j\leq n$}$ .

Existiert eine integrierbare Funktion $\mbox{$f:\mathbb{R}\longrightarrow [0,\infty)$}$ mit

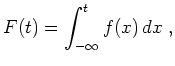
$\mbox{$\displaystyle F(t) = \int_{-\infty}^t f(x)\,dx\; , $}$

so heißt $\mbox{$f$}$ die Dichte von $\mbox{$X$}$ .

Der Erwartungswert von $\mbox{$X$}$ ist dann definiert als

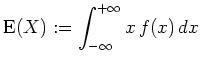
$\mbox{$\displaystyle {\operatorname{E}}(X) := \int_{-\infty}^{+\infty} x\, f(x)\, dx $}$

falls dieses Integral absolut konvergiert.

Ist $\mbox{$X$}$ diskret verteilt, d.h. $\mbox{$X(\Omega) = \{ t_i\; \vert\; i\in I\subseteq \mathbb{N}\}$}$ , setzen wir analog

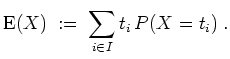
$\mbox{$\displaystyle {\operatorname{E}}(X)\; :=\; \sum_{i\in I} t_i\, P(X = t_i)\; . $}$

Die Varianz $\mbox{${\operatorname{Var}}(X)$}$ , mit der die zu erwartende Abweichung vom Erwartungswert gemessen werden soll, ist definiert als

$\mbox{$\displaystyle {\operatorname{Var}}(X)\; :=\; {\operatorname{E}}\big((X - {\operatorname{E}}(X))^2\big)\; . $}$

Abweichungen vom Erwartungswert werden so quadratisch gewichtet.

Im diskreten Fall ergibt sich also

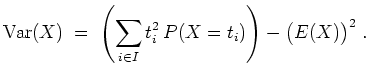
$\mbox{$\displaystyle {\operatorname{Var}}(X)\; =\; \left(\sum_{i\in I} t_i^2\, P(X = t_i)\right) - \bigl(E(X)\bigr)^2 \; . $}$

Es gelten für Zufallsvariablen $\mbox{$X$}$ und $\mbox{$Y$}$ die folgenden Regeln.

$\mbox{${\operatorname{E}}(\lambda X + \mu Y) = \lambda{\operatorname{E}}(X) + \mu{\operatorname{E}}(Y)$}$ für $\mbox{$\lambda,\mu\in\mathbb{R}$}$ .
Ist $\mbox{$X(\omega)\leq Y(\omega)$}$ für alle $\mbox{$\omega\in\Omega$}$ , so ist $\mbox{${\operatorname{E}}(X)\leq{\operatorname{E}}(Y)$}$ .
$\mbox{${\operatorname{Var}}(X) = {\operatorname{E}}(X^2) - \bigl({\operatorname{E}}(X)\bigr)^2$}$ .
$\mbox{${\operatorname{Var}}(\lambda X) = \lambda^2{\operatorname{Var}}(X)$}$ für $\mbox{$\lambda\in\mathbb{R}$}$ .
Falls $\mbox{$X$}$ und $\mbox{$Y$}$ unabhängig sind, gilt $\mbox{${\operatorname{E}}(XY) = {\operatorname{E}}(X){\operatorname{E}}(Y)$}$ , und folglich $\mbox{${\operatorname{Var}}(X+Y) = {\operatorname{Var}}(X) + {\operatorname{Var}}(Y)$}$ .
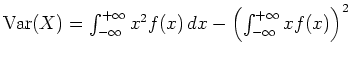Über die Dichte ausgedrückt, gilt $\mbox{${\operatorname{Var}}(X) = \int_{-\infty}^{+\infty} x^2 f(x)\, dx - \left( \int_{-\infty}^{+\infty} x f(x)\right)^2\; $}$ .

(Autoren: Künzer/Meister/Nebe)

Beispiele

Aufgaben

automatisch erstellt am 21.3.2003