Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Repetitorium HM III - Wahrscheinlichkeitsrechnung und Statistik

Gesetze der großen Zahlen und Grenzwertsätze

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]

Gesetze der großen Zahlen

Im folgenden sei $ \mbox{$(X_n)_{n\in\mathbb{N}}$}$ eine unabhängige Folge von Zufallsvariablen.

In der Praxis kann $ \mbox{$X_j$}$ etwa das Meßergebnis der $ \mbox{$j$}$-ten Messung eines beliebig oft wiederholbaren Versuchs darstellen. Liegt etwa daß Meßergebnis stets zwischen $ \mbox{$0$}$ und $ \mbox{$1$}$, so kann man den Wahrscheinlichkeitsraum $ \mbox{$\Omega = [0,1]^{\mathbb{N}}$}$ verwenden. Ein Elementarereignis $ \mbox{$(x_n)_{n\in\mathbb{N}}$}$ ist also eine Folge von Meßwerten. Die Funktion $ \mbox{$X_n:\Omega\longrightarrow \mathbb{R}$}$ greift dann den $ \mbox{$n$}$-ten Meßwert heraus und trägt in auf der Skala $ \mbox{$\mathbb{R}$}$ ab.

Berechnet man eine Größe als Mittelwert von Einzelmessungen, so wird sich dieser Durchschnitt im allgemeinen durch Versuchswiederholung stabilisieren. Im Wahrscheinlichkeitsmodell kann man unter gewissen Voraussetzungen eine solche Stabilisierung mathematisch fassen und beweisen (Gesetze der großen Zahlen).

Das starke Gesetz der großen Zahlen besagt in Worten, daß die Folge der Mittelwerte einer unabhängig verteilten Zufallsvariablenfolge $ \mbox{$(X_n)_{n\in\mathbb{N}}$}$ mit konstantem Erwartungswert $ \mbox{${\operatorname{E}}(X_n) = \mu$}$ und konstanter Varianz $ \mbox{${\operatorname{Var}}(X_n) = \sigma^2$}$ mit Wahrscheinlichkeit $ \mbox{$1$}$ gegen den Erwartungswert $ \mbox{$\mu$}$ konvergiert. Sei hierzu $ \mbox{$\bar X_n = \frac{1}{n}\sum_{k=1}^n X_k$}$ der Mittelwert der ersten $ \mbox{$n$}$ Zufallsvariablen. Es existiert der Mittelwert der ganzen Folge $ \mbox{$\lim_{n\to\infty}\bar X_n$}$ und es gilt

$ \mbox{$\displaystyle P(\lim_{n\to\infty}\bar X_n = \mu) \; =\; 1\; . $}$

Hieraus folgt das schwache Gesetz der großen Zahlen

$ \mbox{$\displaystyle \lim_{n\to\infty} P(\left\vert\bar X_n - \mu\right\vert< \alpha) \; =\; 1\; . $}$
Anders formuliert bedeutet dies, die Folge $ \mbox{$\left(\frac{1}{n}((\sum_{k=1}^n X_k) - n\,\mu)\right)_{n\in\mathbb{N}}$}$ konvergiert mit Wahrscheinlichkeit $ \mbox{$1$}$ gegen $ \mbox{$0$}$.

Zentraler Grenzwertsatz

Betrachte die folgende Dichtefunktion für vorgegebene $ \mbox{$\mu\in\mathbb{R}$}$ und $ \mbox{$\sigma\in\mathbb{R}_{> 0}$}$.

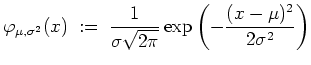
$ \mbox{$\displaystyle \varphi _{\mu,\sigma^2}(x)\; := \; \frac{1}{\sigma\sqrt{2\pi}}\exp\left(-\frac{(x - \mu)^2}{2\sigma^2}\right) $}$
Die zugehörige Verteilungsfunktion werde mit
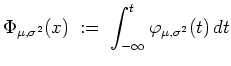
$ \mbox{$\displaystyle \Phi_{\mu,\sigma^2}(x) \; :=\; \int_{-\infty}^t \varphi _{\mu,\sigma^2}(t)\, dt $}$
bezeichnet. Eine Zufallsvariable mit Dichte $ \mbox{$\varphi _{\mu,\sigma^2}$}$ heiße normalverteilt mit Erwartungswert $ \mbox{$\mu$}$ und Varianz $ \mbox{$\sigma^2$}$.

Sind hierbei $ \mbox{$\mu = 0$}$ und $ \mbox{$\sigma^2 = 1$}$, so spricht man von einer Standardnormalverteilung.

Sei $ \mbox{$(X_n)_{n\in\mathbb{N}}$}$ eine identisch und gleichverteilte Folge von Zufallsvariablen mit $ \mbox{${\operatorname{E}}(X_i) = \mu$}$ und $ \mbox{${\operatorname{Var}}(X_i) = \sigma^2 > 0$}$. Identisch verteilt heiße hierbei, daß die zu $ \mbox{$X_n$}$ gehörige Verteilungsfunktion nicht von $ \mbox{$n$}$ abhängt.

Die durch

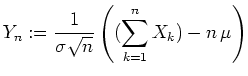
$ \mbox{$\displaystyle Y_n := \frac{1}{\sigma\sqrt{n}}\left((\sum_{k=1}^n X_k) - n\,\mu\right) $}$
neu definierte Folge bekommt durch diese Verschiebung und Skalierung den Erwartungswert $ \mbox{$0$}$ und die Varianz $ \mbox{$1$}$.

Der zentrale Grenzwertsatz besagt nun, daß unabhängig von den weiteren Eigenschaften der Verteilungsfunktion der $ \mbox{$X_k$}$ die Folge $ \mbox{$P(Y_n \leq x)$}$ der Verteilungen der $ \mbox{$Y_n$}$ gegen die Verteilung der Standardnormalverteilung konvergiert, d.h.

$ \mbox{$\displaystyle \lim_{n\to\infty} P(Y_n\leq x) \; =\; \Phi_{0,1}(x) $}$
gilt für alle $ \mbox{$x\in\mathbb{R}$}$. Beachte, daß hingegen über die Konvergenz der Folge $ \mbox{$(Y_n)_{n\in\mathbb{N}}$}$ keine Aussage gemacht wird.

Grenzwertsatz von de Moivre-Laplace

Wir wollen den zentralen Grenzwertsatz nun auf eine unabhängige Folge von Zufallsvariablen $ \mbox{$(X_n)_{n\in\mathbb{N}}$}$ mit

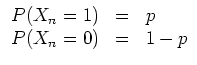
$ \mbox{$\displaystyle \begin{array}{rcl} P(X_n = 1) & = & p \\ P(X_n = 0) & = & 1 - p \\ \end{array}$}$
anwenden, wobei $ \mbox{$p\in (0,1)$}$. Insbesondere ergeben sich so $ \mbox{$E(X_n) = p$}$ und $ \mbox{${\operatorname{Var}}(X_n) = p(1-p)$}$.

Nach dem Grenzwertsatz von de Moivre-Laplace gilt nun für $ \mbox{$x\in\mathbb{R}$}$

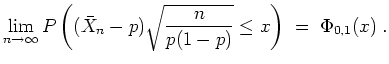
$ \mbox{$\displaystyle \lim_{n\to\infty} P\left((\bar X_n - p)\sqrt{\frac{n}{p(1-p)}}\leq x\right) \; =\; \Phi_{0,1}(x)\; . $}$

In der Praxis wird diese Formel wie folgt für große $ \mbox{$n$}$ zur Approximation von $ \mbox{$P(\bar X_n - y)$}$ verwandt, wobei $ \mbox{$y$}$ entsprechend zu verrechnen ist.

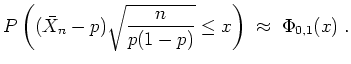
$ \mbox{$\displaystyle P\left((\bar X_n - p)\sqrt{\frac{n}{p(1-p)}}\leq x\right) \; \approx\; \Phi_{0,1}(x)\; . $}$

Grenzwertsatz von Poisson

Sei $ \mbox{$(p_n)_{n\in\mathbb{N}}$}$ eine Folge reeller Zahlen $ \mbox{$p_n\in (0,1)$}$ mit $ \mbox{$\lim_{n\to\infty} n p_n =: \lambda > 0$}$. Dann ist

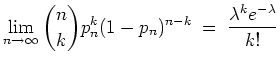
$ \mbox{$\displaystyle \lim_{n\to\infty}\binom{n}{k} p_n^k (1 - p_n)^{n-k} \; =\; \frac{\lambda^k e^{-\lambda}}{k!} $}$
für jede ganze Zahl $ \mbox{$k\geq 0$}$.

Für ein festes $ \mbox{$n\in\mathbb{N}$}$ sei eine unabhängige Folge von Zufallsvariablen $ \mbox{$(X_i)_{i\in\mathbb{N}}$}$ mit

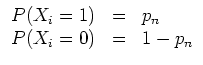
$ \mbox{$\displaystyle \begin{array}{rcl} P(X_i = 1) & = & p_n \\ P(X_i = 0) & = & 1 - p_n \\ \end{array}$}$
gegeben. Dann gilt
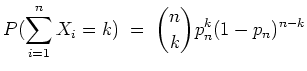
$ \mbox{$\displaystyle P(\sum_{i=1}^n X_i = k) \; =\; \binom{n}{k} p_n^k (1 - p_n)^{n-k} $}$
und somit approximativ
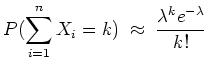
$ \mbox{$\displaystyle P(\sum_{i=1}^n X_i = k) \;\approx\; \frac{\lambda^k e^{-\lambda}}{k!} $}$
mit $ \mbox{$\lambda = n\, p_n$}$.

(Autoren: Künzer/Meister/Nebe)

Beispiele

Aufgaben

  automatisch erstellt am 21.3.2003