Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Repetitorium HM III - Codierungstheorie

Endliche Körper

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]

Codierungstheorie bedient sich der Linearen Algebra über endlichen Körpern.

Ringe und Körper

Ein Ring ist eine Menge $ \mbox{$R$}$, zusammen mit Operationen $ \mbox{$+$}$ und $ \mbox{$\cdot$}$, welche Assoziativ-, Kommutativ- und Distibutivgesetze erfüllen. Ferner hat ein Ring eine $ \mbox{$0$}$ und eine $ \mbox{$1$}$, und zu jedem $ \mbox{$x\in R$}$ gibt es ein $ \mbox{$-x\in R$}$ mit $ \mbox{$x + (-x) = 0$}$.

Hat jedes Element $ \mbox{$x\in R\backslash \{ 0\}$}$ auch ein multiplikativ Inverses $ \mbox{$x^{-1}$}$, gilt also $ \mbox{$x\cdot x^{-1} = 1$}$, so heißt $ \mbox{$R$}$ ein Körper.

Zum Beispiel bilden die ganzen Zahlen $ \mbox{$\mathbb{Z}$}$ einen Ring, aber keinen Körper. Beispiele für Körper sind die rationalen Zahlen $ \mbox{$\mathbb{Q}$}$, die reellen Zahlen $ \mbox{$\mathbb{R}$}$ und die komplexen Zahlen $ \mbox{$\mathbb{C}$}$.

Ist $ \mbox{$R$}$ ein Ring, so bezeichnet $ \mbox{$R[X]$}$ den Polynomring über $ \mbox{$R$}$ in der Unbestimmten $ \mbox{$X$}$. Seine Elemente sind Polynome mit Koeffizienten in $ \mbox{$R$}$, Addition und die Multiplikation sind die für Polynome gebräuchlichen.

Vorsicht, ein Polynom ist ein formaler Ausdruck, der erst durch Einsetzen von Werten für $ \mbox{$X$}$ eine Funktion von $ \mbox{$R$}$ nach $ \mbox{$R$}$ definiert. Für gewisse Grundringe $ \mbox{$R$}$ ist es möglich, daß zwei verschiedene Polynome auf diese Weise dieselbe Funktion definieren.

Ein Ideal $ \mbox{$I$}$ in einem Ring $ \mbox{$R$}$ ist eine Teilmenge, die folgende Eigenschaften erfüllt.

Zum Beispiel bildet die Menge der geraden Zahlen $ \mbox{$2\mathbb{Z}$}$ ein Ideal in $ \mbox{$\mathbb{Z}$}$. Oder aber, $ \mbox{$(X^2 + 1)\mathbb{R}[X]$}$ bildet ein Ideal in $ \mbox{$\mathbb{R}[X]$}$.

Jedes Ideal $ \mbox{$I$}$ in $ \mbox{$R$}$ definiert nun einen neuen Ring, den Restklassenring $ \mbox{$R/I$}$. Formal sind dessen Elemente Äquivalenzklassen von Elementen aus $ \mbox{$R$}$, wobei $ \mbox{$x\sim y$}$ falls $ \mbox{$x - y\in I$}$. Addition und Multiplikation sind repräsentantenweise definiert.

In der Praxis rechnet man in $ \mbox{$R/I$}$ mit den Elementen aus $ \mbox{$R$}$, nur unter Berücksichtigung der Tatsache, daß die Elemente in $ \mbox{$I$}$ alle verschwinden. Insbesondere kann man während einer Rechnung die einzelnen Terme beliebig modulo $ \mbox{$I$}$ abändern. Von der Äquivalenzklassendefinition merke man sich in erster Linie, daß auf diese Weise die Zahl der Elemente von $ \mbox{$R/I$}$ als Zahl der Äquivalenzklassen in $ \mbox{$R$}$ ermittelt werden kann.

Zum Beispiel hat $ \mbox{$\mathbb{Z}/2\mathbb{Z}$}$ die Elemente $ \mbox{$2\mathbb{Z}= \{\dots,-2,0,2,\dots\}$}$ und $ \mbox{$1 + 2\mathbb{Z}= \{\dots,-1,1,\dots\}$}$. Es wird in $ \mbox{$\mathbb{Z}/2\mathbb{Z}$}$ repräsentantenweise

$ \mbox{$\displaystyle 3\cdot (5 + 7) + 4 \; =\; 1\cdot (1 + 1) + 0 \; =\; 1\cdot 0 + 0 \; =\; 0\; , $}$
da Änderungen modulo $ \mbox{$2\mathbb{Z}$}$ ja erlaubt sind. Weniger geschickt, aber genauso richtig ist es,
$ \mbox{$\displaystyle 3\cdot (5 + 7) + 4 \; =\; 40 \; =\; 0 $}$
zu rechnen.

Endliche Körper

Wir definieren nun zunächst die endlichen Primkörper als $ \mbox{$\mathbb{F}_p := \mathbb{Z}/p\mathbb{Z}$}$ für alle Primzahlen $ \mbox{$p$}$.

Ein Polynom $ \mbox{$f(X) = X^k + a_{k-1} X^{k-1} + \cdots + a_0$}$ in $ \mbox{$\mathbb{F}_p[X]$}$ heißt irreduzibel, falls es sich nicht als Produkt zweier Polynome von echt kleinerem Grad schreiben läßt. Das läßt sich in der Praxis oft nur durch Testen aller potentieller Divisoren mittels Polynomdivision entscheiden.

So ist zum Beispiel $ \mbox{$X^2 + 1\in\mathbb{F}_3[X]$}$ irreduzibel. Wäre es reduzibel, so hätte es einen Linearfaktor der Form $ \mbox{$X - a$}$ als Teiler, und somit $ \mbox{$a$}$ als Nullstelle. Das Polynom $ \mbox{$X^2 + 1$}$ hat aber keine Nullstelle in $ \mbox{$\mathbb{F}_3$}$.

Dahingegen ist $ \mbox{$X^2 + 1\in\mathbb{F}_2[X]$}$ reduzibel, und zwar als $ \mbox{$X^2 + 1 = (X + 1)\cdot (X + 1)$}$.

Ist $ \mbox{$f(X) = X^k + a_{k-1} X^{k-1} + \cdots + a_0$}$ irreduzibel, so bildet $ \mbox{$\mathbb{F}_{p^k} := \mathbb{F}_p[X]/f(X)\mathbb{F}_p[X]$}$ einen Körper. Die Bezeichnung als $ \mbox{$\mathbb{F}_{p^k}$}$ rechtfertigt sich dadurch, daß man zeigen kann, daß dieser Körper im wesentlichen nur vom Grad $ \mbox{$k$}$ des irreduziblen Polynoms abhängt. Umgekehrt kann man zeigen, daß für alle Primzahlen $ \mbox{$p$}$ und für alle $ \mbox{$k\geq 1$}$ wenigstens ein irreduzibles Polynom von Grad $ \mbox{$k$}$ in $ \mbox{$\mathbb{F}_p[X]$}$ existiert (im allgemeinen sogar recht viele). Kurz,

für jede Primpotenz $ \mbox{$p^k$}$ existiert im wesentlichen genau ein Körper $ \mbox{$\mathbb{F}_{p^k}$}$.

Es ist $ \mbox{$\mathbb{F}_p\subseteq \mathbb{F}_{p^k}$}$, indem Konstanten mit Polynomen von Grad $ \mbox{$0$}$ identifiziert werden. So wird $ \mbox{$\mathbb{F}_{p^k}$}$ auch ein Vektorraum über $ \mbox{$\mathbb{F}_p$}$, mit Basis $ \mbox{$\{1,X,X^2,\dots,X^{k-1}\}$}$. In der Tat ergibt sich mit Polynomdivision durch $ \mbox{$f(X)$}$ allgemein in $ \mbox{$\mathbb{F}_p[X]$}$

$ \mbox{$\displaystyle g(X)\; =\; t(X) f(X) + r(X) \; , $}$
wobei der Grad des Restes $ \mbox{$r(X)$}$ kleiner als $ \mbox{$k$}$ ist, und somit in $ \mbox{$\mathbb{F}_{p^k}$}$
$ \mbox{$\displaystyle g(X)\; =\; r(X) \; . $}$
Speziell gilt etwa die Rechenregel
$ \mbox{$\displaystyle X^k \; =\; 1\cdot(X^k + a_{k-1} X^{k-1} + \cdots + a_0) ... ..._{k-1} X^{k-1} + \cdots + a_0) \; =\; - (a_{k-1} X^{k-1} + \cdots + a_0)\; . $}$
Ein Vektorraum der Dimension $ \mbox{$k$}$ über $ \mbox{$\mathbb{F}_p$}$ hat aber $ \mbox{$p^k$}$ Elemente, namentlich alle Polynome von Grad kleiner $ \mbox{$k$}$. Kurz,
$ \mbox{$\mathbb{F}_{p^k}$}$ hat $ \mbox{$p^k$}$ Elemente.

Beachte, daß sich der Restklassenring $ \mbox{$\mathbb{Z}/p^k\mathbb{Z}$}$, der ebenfalls $ \mbox{$p^k$}$ Elemente enthält, im Falle $ \mbox{$k\geq 2$}$ wesentlich von $ \mbox{$\mathbb{F}_{p^k}$}$ unterscheidet. Zum Beispiel gilt für $ \mbox{$x\in\mathbb{F}_{p^k}$}$ stets $ \mbox{$\underbrace{x + x + \cdots + x}_{p\;\text{ Summanden}} = 0$}$. Dies ist zum Beispiel für $ \mbox{$x = 1\in\mathbb{Z}/p^k\mathbb{Z}$}$ falsch falls $ \mbox{$k\geq 2$}$.

Primitive Elemente, Zech-Logarithmen

Jedes Element $ \mbox{$x$}$ in $ \mbox{$\mathbb{F}_{p^k}\backslash\{0\}$}$ erfüllt $ \mbox{$x^{p^k-1} = 1$}$. Ist $ \mbox{$p^k-1$}$ der minimale Exponent $ \mbox{$\geq 1$}$, der $ \mbox{$x$}$ zu $ \mbox{$1$}$ macht, so heißt $ \mbox{$x$}$ primitiv. Man kann zeigen, daß jeder Körper der Form $ \mbox{$\mathbb{F}_{p^k}$}$ wenigstens ein primitives Element enthält. (Ein zufällig ausgewähltes Element wird mit guter Wahrscheinlichkeit primitiv sein.)

Bezüglich eines fest gewählten primitiven Elements $ \mbox{$\alpha\in\mathbb{F}_{p^k}$}$ werden die Zech-Logarithmen wie folgt definiert. Ist $ \mbox{$1 + \alpha^m = \alpha^l$}$, so heißt $ \mbox{$l\in [1,p^k - 2]$}$ der Zech-Logarithmus von $ \mbox{$m\in [0,p^k - 2]$}$. Dies legt $ \mbox{$l$}$ eindeutig fest, es sei denn, es war $ \mbox{$\alpha^m = -1$}$. Diesenfalls setzen wir $ \mbox{$l = -1$}$.

Für die Addition sind diese Zech-Logarithmen hilfreich, da für $ \mbox{$\alpha^j\neq -\alpha^i$}$

$ \mbox{$\displaystyle \alpha^i + \alpha^j\; =\; \alpha^i (1 + \alpha^{j-i}) \; =\; \alpha^{i + l}\; , $}$
wenn $ \mbox{$l$}$ der Zech-Logarithmus von $ \mbox{$j - i$}$ ist. Falls $ \mbox{$\alpha^j = -\alpha^i$}$, so erhalten wir $ \mbox{$l = -1$}$, was bedeutet, daß wir diese Formel nicht anwenden dürfen und stattdessen das Resultat $ \mbox{$0$}$ erhalten.

Betrachten wir einmal den Körper $ \mbox{$\mathbb{F}_4 := \mathbb{F}_2[X]/(X^2 + X + 1)\mathbb{F}_2[X]$}$. Als primitives Element kommt etwa $ \mbox{$\alpha = X$}$ in Frage. In der Tat $ \mbox{$\alpha^1 = X$}$, $ \mbox{$\alpha^2 = X + 1$}$ und $ \mbox{$\alpha^3 = 1$}$. Die diesbezüglichen Zech-Logarithmen können der Tabelle

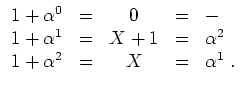
$ \mbox{$\displaystyle \begin{array}{rcccl} 1 + \alpha^0 & = & 0 & = & - \\ 1... ... & = & \alpha^2 \\ 1 + \alpha^2 & = & X & = & \alpha^1\; . \\ \end{array}$}$
entnommen werden. Insbesondere ist der Zech-Logarithmus von $ \mbox{$m = 0$}$ vereinbarungsgemäß $ \mbox{$l = -1$}$. Es wird zum Beispiel $ \mbox{$\alpha^1 + \alpha^2 = \alpha(1 + \alpha^1) = \alpha^{1 + 2} = 1$}$.

Frobenius

Der Frobenius-Automorphismus von $ \mbox{$\mathbb{F}_{p^k}$}$ ist eine bijektive Selbstabbildung von $ \mbox{$\mathbb{F}_{p^k}$}$, gegeben durch $ \mbox{$F(x) = x^p$}$. Es gilt $ \mbox{$F(xy) = F(x)F(y)$}$ für $ \mbox{$x,y\in\mathbb{F}_{p^k}$}$, insbesondere also $ \mbox{$F(ay) = a F(y)$}$ falls $ \mbox{$a\in\mathbb{F}_p$}$. Ferner ist $ \mbox{$F(x + y) = F(x) + F(y)$}$. 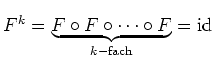Iteriertes Anwenden liefert $ \mbox{$F^k = \underbrace{F\circ F\circ \cdots\circ F}_{k-\text{fach}} = {\mbox{id}}$}$.

(Autoren: Künzer/Meister/Nebe)

Beispiele

Aufgaben

  automatisch erstellt am 21.3.2003