Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Repetitorium HM III - Codierungstheorie

Codes

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]

Allgemeine Codes.

Gegeben sei eine endlich Menge $ \mbox{$A$}$ von $ \mbox{$\geq 2$}$ Elmenten, genannt Alphabet. Ein Code $ \mbox{$C$}$ der Länge $ \mbox{$N\geq 1$}$ ist eine Teilmenge von $ \mbox{$A^N$}$.

Die Informationsrate von $ \mbox{$C$}$ ist

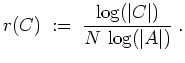
$ \mbox{$\displaystyle r(C) \;:=\; \frac{\log(\vert C\vert)}{N\,\log(\vert A\vert)}\;. $}$

Für $ \mbox{$x,y\in A^N$}$ ist die Hamming-Distanz von $ \mbox{$x=(x_1,\dots,x_N)$}$ und $ \mbox{$y=(y_1,\dots,y_N)$}$ definiert durch

$ \mbox{$\displaystyle d(x,y) \;:=\; \vert\{i\in\{1,\dots,N\}\;:\;x_i \neq y_i\}\vert\;. $}$
Der minimale Abstand zweier verschiedener Wörter in $ \mbox{$C$}$ heißt Minimaldistanz $ \mbox{$d(C)$}$ von $ \mbox{$C$}$.

Ein Minimal-Distanz-Decodierer (MDD) liefert zu jedem $ \mbox{$a\in A^N$}$ ein Codewort $ \mbox{$c\in C$}$, das zu $ \mbox{$a$}$ minimale Hamming-Distanz hat. Ein MDD ist also eine Funktion $ \mbox{$f:A^N\longrightarrow C$}$ mit

$ \mbox{$\displaystyle d(f(a),a) = \min\{d(c,a):c\in C\} $}$
für alle $ \mbox{$a\in A^N$}$.

Zwei Codes $ \mbox{$C$}$ und $ \mbox{$C'$}$ heißen äquivalent, falls es eine Permutation $ \mbox{$\sigma$}$ auf $ \mbox{$\{1,\dots,N\}$}$ so gibt, daß $ \mbox{$\ c = (c_1,\dots,c_n) \mapsto (c_{\sigma(1)}, \dots,c_{\sigma(N)})$}$ eine Bijektion von $ \mbox{$C$}$ nach $ \mbox{$C'$}$ darstellt. Äquivalente Codes haben dieselbe Informationsrate und dieselbe Minimaldistanz.

Ziel der Codierungstheorie ist es, Codes mit großem Minimalabstand bei großer Informationsrate zu finden.

Lineare Codes.

Sei im folgenden $ \mbox{$A=\mathbb{F}_{p^k}$}$ ein endliche Körper und $ \mbox{$A^N$}$ der Vektorraum der Dimension $ \mbox{$N$}$ über $ \mbox{$A$}$. Ein Untervektorraum $ \mbox{$C$}$ von $ \mbox{$A^N$}$ heißt linearer Code. Ist $ \mbox{$(b_1,\dots,b_k)$}$ eine Basis von $ \mbox{$C$}$, geschrieben als Zeilenvektoren, so heißt die Matrix $ \mbox{$B\in A^{k\times N}$}$ mit den Zeilen $ \mbox{$b_1,\dots,b_k$}$ eine Erzeugermatrix von $ \mbox{$C$}$.

Ein linearer Code $ \mbox{$C\subseteq A^N$}$ der Dimension $ \mbox{$k$}$ hat die Informationsrate $ \mbox{$r(C) = \frac{k}{N}$}$. Ist die Minimaldistanz $ \mbox{$d=d(C)$}$, so spricht man von einem $ \mbox{$[N,k,d]$}$-Code. Der Minimalabstand eines linearen Codes ist gleich der minimalen Anzahl der Nichtnulleinträge eines Codeworts ungleich dem Nullvektor.

Sei $ \mbox{$C$}$ ein linearer Code von Dimension $ \mbox{$k$}$, dann ist $ \mbox{$C$}$ äquivalent zu einem linearen Code mit einer Erzeugermatrix $ \mbox{$(E_k\vert P_{N-k})$}$, wobei $ \mbox{$E_k\in A^{k\times k}$}$ die Einheitsmatrix bezeichnet.

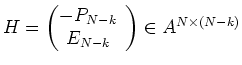Für einen linearen Code $ \mbox{$C$}$ mit einer Erzeugermatrix $ \mbox{$G =(E_k\vert P_{N-k})\in A^{k\times N}$}$ ist eine Prüfmatrix durch $ \mbox{$H=\left(\begin{matrix}-P_{N-k}\\ E_{N-k}\end{matrtix}\right)\in A^{N\times(N-k)}$}$ gegeben.

Allgemein heißt jede Matrix $ \mbox{$H\in\A^{N\times(N-K)}$}$, die

erfüllt, eine Prüfmatrix zu $ \mbox{$C$}$.

Ist $ \mbox{$c\in C$}$ ein Codewort und $ \mbox{$e\in A^N$}$ ein Übermittlungsfehler, so liefert die Multiplikation mit der Prüfmatrix

$ \mbox{$\displaystyle (c+e)H\;=\;cH + eH\;=\;eH $}$
das Syndrom $ \mbox{$eH$}$ von $ \mbox{$c+e$}$.

Ein MDD für einen linearen Code $ \mbox{$C$}$ ist definiert durch $ \mbox{$f(a) = a - a'$}$ wobei $ \mbox{$a'$}$ in Abhängigkeit von $ \mbox{$a$}$ so gewählt ist, daß das Syndrom $ \mbox{$a'H=aH$}$ wird, und so, daß $ \mbox{$d(a',0) = \min\{d(x,0)\;:\; x\in A^N,\; xH = aH\}$}$.

(Ist $ \mbox{$\frac{d(C)}{2}$}$ größer als die Übertragungsfehlerzahl, so wird man für $ \mbox{$a = c+e$}$ wie oben auf diese Weise auf $ \mbox{$a' = e$}$ stoßen.)

Binäre Hamming-Codes.

Ein binärer Hamming-Code der Länge $ \mbox{$N=2^r-1$}$ (mit $ \mbox{$r\in\mathbb{N}$}$) ist bestimmt durch eine Prüfmatrix $ \mbox{$H\in\mathbb{F}_2^{N\times r}$}$, wobei in den Zeilen gerade alle Vektoren von $ \mbox{$\mathbb{F}_2^r\backslash\{0\}$}$ stehen. Hamming-Codes sind $ \mbox{$[N,N-r,3]$}$-Codes. Der für die Praxis entscheidende Vorteil ist die einfache Fehlerkorrektur bei der Decodierung. Bei binären Hamming-Codes ist für $ \mbox{$a\in\mathbb{F}_2^N$}$ das Syndrom $ \mbox{$aH$}$ an höchstens einer Stelle nicht Null, und der (eindeutige) MDD ist gegeben durch

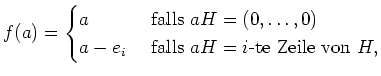
$ \mbox{$\displaystyle f(a) = \begin{cases} a & \text{ falls } aH = (0,\dots, 0)\\ a - e_i & \text { falls } aH = i\text{-te Zeile von } H, \end{cases}$}$
wobei $ \mbox{$e_i$}$ den $ \mbox{$i$}$-ten Einheitsvektor von $ \mbox{$\mathbb{F}_2^N$}$ bezeichnet. Tritt bei der Übertragung mehr als ein Fehler auf, so wird zu einem ,,falschen`` Codewort decodiert.

(Autoren: Künzer/Meister/Nebe)

Beispiele

Aufgaben

  automatisch erstellt am 21.3.2003