Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Repetitorium HM III - Codierungstheorie

Zyklische Codes

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]

Erzeugerpolynome.

Im folgenden sei $ \mbox{$q=p^f$}$ eine Primzahlpotenz und $ \mbox{$\mathbb{F}_q$}$ der Körper mit $ \mbox{$q$}$ Elementen.

Ein linearer Code $ \mbox{$C\subset\mathbb{F}_q^N$}$ heißt zyklisch, falls

$ \mbox{$\displaystyle (c_0,\dots,c_{N-1})\in C\;\Rightarrow\;(c_{N-1},c_0,c_1,\dots,c_{N-2})\in C. $}$
Ein zyklischer Code wird durch ein Ideal in $ \mbox{$B:=\mathbb{F}_q[X]/(X^N-1)\mathbb{F}_q[X]$}$ beschrieben; jedes Codewort $ \mbox{$c=(c_0,\dots, c_{N-1})\in\mathbb{F}_q^N$}$ wird mit
$ \mbox{$\displaystyle (c_0,c_1,\dots,c_n)= c_0 + c_1 X + \dots+c_{N-1}X^{N-1}\in B $}$
identifiziert.

Im folgendem sei $ \mbox{$N$}$ kein Vielfaches von $ \mbox{$p$}$. Ausgehend von einer Faktorisierung in $ \mbox{$\mathbb{F}_q[X]$}$

$ \mbox{$\displaystyle X^N-1 = f_{(1)}(X)\cdots f_{(t)}(X) \in \mathbb{F}_q[X] $}$
in paarweise verschiedene, normierte und irreduzible $ \mbox{$f_{(i)}\in\mathbb{F}_q[X]$}$, sind die Ideale von $ \mbox{$R$}$ von der Form
$ \mbox{$\displaystyle f_{(i_1)}\cdots f_{(i_s)}R, $}$
wobei $ \mbox{$0\leq s\leq t$}$ und $ \mbox{$1\leq i_1<i_2<\dots<i_s\leq t$}$.

Ein solches Polynom $ \mbox{$g:=f_{(i_1)}\cdots f_{(i_s)}=\sum_{j=0}^{N-k}g_jX^j$}$ vom Grade $ \mbox{$N-k$}$ heißt Erzeugerpolynom des zyklischen Codes $ \mbox{$C_g:=gR\subseteq R$}$ mit Dimension $ \mbox{$k$}$. Eine Erzeugermatrix ist

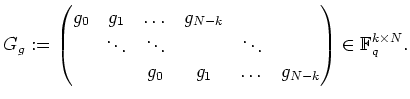
$ \mbox{$\displaystyle G_g:=\begin{pmatrix} g_0 & g_1 & \dots & g_{N-k} & \\ ... ... & & g_0 & g_1 & \dots & g_{N-k} \end{pmatrix}\in\mathbb{F}_q^{k\times N}. $}$
Das Polynom $ \mbox{$h=\sum_{j=0}^{k}h_j X^j\in\mathbb{F}_p[X]$}$ mit $ \mbox{$gh=X^N-1$}$ heißt Prüfpolynom von $ \mbox{$C_g$}$. Eine Prüfmatrix ist
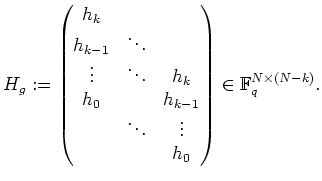
$ \mbox{$\displaystyle H_g:=\begin{pmatrix} h_k & & \\ h_{k-1} & \ddots & \... ...& \ddots & \vdots \\ & & h_0 \end{pmatrix}\in\mathbb{F}_q^{N\times(N-k)}. $}$

Minimalabstand bei zyklischen Codes.

Der Minimalabstand bei zyklischen Codes ist i.a. schwierig zu bestimmen; folgende Abschätzung ist jedoch bekannt.

Bezeichne $ \mbox{$\varphi(N)$}$ die Anzahl der zu $ \mbox{$N$}$ teilerfremden Zahlen in $ \mbox{$\{1,\dots,N\}$}$.

Ist $ \mbox{$\alpha$}$ eine Nullstelle in $ \mbox{$\mathbb{F}_{q^{\varphi(N)}}$}$ von $ \mbox{$X^N-1\in\mathbb{F}_q[X]$}$ mit $ \mbox{$N=\min\{n\in\mathbb{N}:\alpha^n=1\}$}$, so heißt $ \mbox{$\alpha$}$ eine primitive $ \mbox{$N$}$-te Einheitswurzel über $ \mbox{$\mathbb{F}_q$}$.

Sei ein zyklischer Code $ \mbox{$C_g \subseteq R$}$ und eine primitve $ \mbox{$N$}$-te Einheitswurzel $ \mbox{$\alpha$}$ gegeben. Gilt dann $ \mbox{$g(\alpha^b)=0, g(\alpha^{b+1})=0, \dots, g(\alpha^{b+\delta-2})=0$}$ für eine Wahl von $ \mbox{$b\in\mathbb{N}$}$, $ \mbox{$\delta \geq 2$}$ so folgt $ \mbox{$d(C_g) \geq \delta$}$.

Codierung bei zyklischen Codes.

Um bei einem zyklischen Code $ \mbox{$C_g$}$ mit $ \mbox{$g=\sum_{j=0}^{N-k}g_jX^j$}$, Länge $ \mbox{$N$}$ und Dimension $ \mbox{$k$}$ ein Informationswort $ \mbox{$u=(u_0,\dots,u_{k-1})\in\mathbb{F}_q^k$}$ einem Codewort $ \mbox{$c=(c_0,\dots, c_{N-1})\in\mathbb{F}_q^N$}$ zuzuweisen, können die Kontrollbits mit Hilfe von Polynomdivision berechnet werden. Dabei wird das Informationswort zunächst als Element aus $ \mbox{$\mathbb{F}_q[X]$}$ dargestellt,

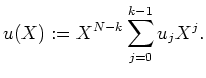
$ \mbox{$\displaystyle u(X) := X^{N-k} \sum_{j=0}^{k-1} u_jX^j. $}$
Polynomdivision von $ \mbox{$u(X)$}$ durch $ \mbox{$g(X)$}$ ergibt einen Rest $ \mbox{$r(X)=\sum_{j=0}^{N-k-1}r_jX^j\in\mathbb{F}_q[X]$}$.

Man verwendet dann als Codewort $ \mbox{$c = (-r_0,\dots,-r_{N-k-1},u_0,\dots,u_{k-1})$}$.

Unvollständiges Decodieren.

Gegeben sei ein Erzeugerpolynom $ \mbox{$g$}$ für den zyklischen Code $ \mbox{$C_g \subseteq R$}$ der Länge $ \mbox{$N$}$ so, daß mit einer primitiven $ \mbox{$N$}$-ten Einheitswurzel $ \mbox{$\alpha\in\mathbb{F}_{q^{\varphi(N)}}$}$ und $ \mbox{$\delta \geq 2$}$ das Erzeugerpolynom die Nullstellen $ \mbox{$g(\alpha^b) = g(\alpha^{b+1}) = \dots = g(\alpha^{b+\delta -2}) = 0$}$ hat. Ist $ \mbox{$\delta = 2t+1$}$, so gilt $ \mbox{$d(C_g)\geq 2t+1$}$ und es können bis zu $ \mbox{$t$}$ Fehler decodiert werden. Allerdings gibt es i.a. Elemente $ \mbox{$a\in\mathbb{F}_q^N$}$, die nicht decodiert werden können.

Das Verfahren wird besonders übersichtlich, wenn folgende Vereinfachungen vorausgesetzt werden. Seien $ \mbox{$\alpha,\dots,\alpha^{2t}$}$ Nullstellen von $ \mbox{$g$}$. Es seien ferner das Codewort $ \mbox{$c=(c_0,c_1,\dots,c_{N-1})$}$ und das empfangene Wort

$ \mbox{$\displaystyle r = (r_0,r_1,\dots,r_{N-1}) &=& r_0 + r_1X + \cdots + r_NX^{N-1} $}$
in höchstens $ \mbox{$t$}$ Stellen verschieden.

Dann können Koeffizienten für die Polynome

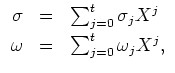
$ \mbox{$\displaystyle \begin{array}{rcl} \sigma &=& \sum_{j=0}^t \sigma_j X^j\vspace*{1mm}\\ \omega &=& \sum_{j=0}^t \omega_j X^j, \end{array}$}$
wobei $ \mbox{$\sigma_0=1$}$ und $ \mbox{$\omega_0=0$}$ vorausgesetzt werden können, durch Lösen eines Gleichungssystems in $ \mbox{$\mathbb{F}_q$}$ eindeutig so bestimmt werden, daß die Potenzreihenentwicklung von $ \mbox{$\frac{\omega(X)}{\sigma(X)}$}$ mit $ \mbox{$\sum_{l=1}^{2t} r(\alpha^l)X^l$}$ beginnt, und der Grad von $ \mbox{$\omega$}$ kleiner oder gleich dem Grad von von $ \mbox{$\sigma$}$ ist.

Ist $ \mbox{$\sigma(\alpha^{-i})=0$}$, so ist die $ \mbox{$i$}$-te Stelle des empfangenen Wortes durch die Übertragung verlorengegangen und wird durch

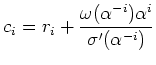
$ \mbox{$\displaystyle c_i = r_i + \frac{\omega(\alpha^{-i})\alpha^i}{\sigma'(\alpha^{-i})} $}$
korrigiert, wobei $ \mbox{$\sigma'(X)$}$ die Ableitung nach $ \mbox{$X$}$ von $ \mbox{$\sigma(X)\in\mathbb{F}_q[X]$}$ bezeichnet.

(Autoren: Künzer/Meister/Nebe)

Beispiele

Aufgaben

  automatisch erstellt am 21.3.2003