Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Formelsammlung - Lineare Algebra

Grundlegende Strukturen

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Gruppe Assoziativgesetz: $ a \diamond (b\diamond c) = (a\diamond b) \diamond c$
  Neutrales Element: $ a\diamond e = e \diamond a = a$
  Inverses Element: $ a \diamond a^{-1} = a^{-1} \diamond a = e$
   
abelsche Gruppe kommutativ: $ a\diamond b = b \diamond a$
   
Körper $ (K,+) $ ist abelsche Gruppe

$ (K \backslash \{0\}, \cdot)$ ist abelsche Gruppe

Distributivgesetz: $ a\cdot (b+c) = a\cdot b + a \cdot c$
   
Vektorraum abelsche Gruppe $ (V,+) $ über Skalarkörper $ K$
  $ (\lambda_1 + \lambda_2)\cdot v = \lambda_1\cdot v + \lambda_2\cdot v$
  $ \lambda\cdot(v_1+v_2) = \lambda\cdot v_1 + \lambda\cdot v_2$
  $ (\lambda_1\,\lambda_2)\cdot v = \lambda_1\cdot(\lambda_2\cdot v)$
  $ 1 \cdot v = v $
   
Skalarprodukt $ \langle v,v \rangle > 0$ für $ v\ne 0$
  $ \langle u,v \rangle = \overline{\langle v,u\rangle}$
  $ \langle \lambda u, v \rangle = \lambda \langle u, v \rangle$
  $ \langle u+v, w \rangle = \langle u,w\rangle + \langle v,w\rangle$
   
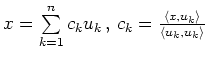orthogonale Basis $ x=\sum\limits_{k=1}^n c_ku_k\,,\,c_k=\frac{\langle x,u_k\rangle}{\langle u_k,u_k\rangle}$
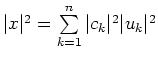  $ \vert x\vert^2=\sum\limits_{k=1}^n \vert c_k\vert^2\vert u_k\vert^2$
   
Cauchy-Schwarz $ \vert\langle u,v\rangle \vert \leq \vert u\vert\vert v\vert\,,\vert u\vert=\sqrt{\langle u,u\rangle}$
   
Norm $ \left\Vert v\right\Vert > 0\,,\,v\neq 0$
  $ \left\Vert\lambda\, v\right\Vert = \vert\lambda\vert\,\left\Vert v\right\Vert$
  $ \left\Vert u+v\right\Vert \leq \left\Vert u\right\Vert + \left\Vert v\right\Vert$
   
Lineare Abbildung Additivität:      $ L(v_1+v_2) = L(v_1) + L(v_2)$
  Homogenität:      $ L(\lambda v) = \lambda \, L(v)$
   
Bild und Kern Bild $ (L) = \{w\in W \,:\; \exists v \in V$    mit $ L(v) = w\}$
  ker $ (L) = \{v \in V \,:\; L(v) = 0 \}$
  dim $ V$ = dim ker($ L$) + dim Bild($ L$)
   
(Autor: M. Reble)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 31.1.2006