Mathematik-Online-Kurs: Formelsammlung-Lineare Algebra-Matrizen

	[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
	Mathematik-Online-Kurs: Formelsammlung - Lineare Algebra
	Matrizen

[vorangehende Seite] [nachfolgende Seite]

[Gesamtverzeichnis][Seitenübersicht]

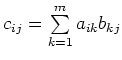Matrix-Multiplikation	$c_{ij} = \sum\limits_{k=1}^{m}a_{ik}b_{kj}$
	$A(BC) = (AB)C, \quad (AB)^{-1} = B^{-1}A^{-1}, \quad (AB)^* = B^A^$
Kommutator	$\left[A,B\right]$ =
Rang	Anzahl linear unabhängiger Zeilen / Spalten $\operatorname{Rang}\,A = \operatorname{Rang}\,A^{\operatorname t}$ $\operatorname{Rang}\,(BAC)=\operatorname{Rang}\,(A)$ , ( invertierbar)
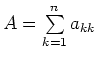Spur	Summe der Diagonalelemente: Spur $A=\sum\limits_{k=1}^n a_{kk}$
	Spur Spur
hermitesch (symmetrisch)	( $A^{\operatorname t}= A$ ) nur reelle Eigenwerte, es gibt ONB aus Eigenvektoren
unitär (orthogonal)	$A^* = A^{-1}$ ( $A^{\operatorname t}= A^{-1}$ ) $\vert\operatorname{det}\,A\vert=1$ , Spalten bilden ONB
normal	$\Leftrightarrow$ unitär diagonalisierbar
Drehmatrix	orthogonal und $\operatorname{det}\,A=1$ Drehachse ist Eigenvektor zum Eigenwert 1 Drehwinkel: $\cos\alpha = \frac{1}{2}(\operatorname{Spur}\,A-1)$
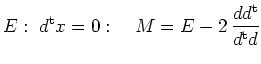
Spiegelung	Ebene $\displaystyle E:\; d^{\operatorname t}x = 0: \quad M = E - 2\,\frac{dd^{\operatorname t}}{d^{\operatorname t}d}$ Gerade $\displaystyle G:\; x = \lambda v: \quad M = 2\,\frac{vv^{\operatorname t}}{v^{\operatorname t}v} - E$

Eigenwerte / -vektoren $Av = \lambda v \,, \; v \neq 0 \Leftrightarrow \operatorname{det}(A-\lambda E) = 0$

$\sum\lambda_i = \operatorname{Spur} A\,, \quad \prod\lambda_i = \operatorname{det} A$

$A^{\operatorname t}$ hat Eigenwert $\lambda$
$A^{-1}$ hat Eigenvektor und Eigenwert $1/\lambda$
hat Eigenvektor und Eigenwert $\lambda^n$
$Q^{-1}AQ$ hat Eigenvektor $Q^{-1}v$ und Eigenwert $\lambda$

Diagonalisierung für alle Eigenwerte: algebr. = geometr. Vielfachheit
$B^{-1}AB = \operatorname{diag}(\lambda_1,\ldots,\lambda_n)$
$B = (b_1,\ldots,b_n)$ Basis aus Eigenvektoren

Jordan-Form Blockdiagonalmatrix $J = B^{-1} A B = \operatorname{diag}(J_1,\ldots,J_m)$
Blöcke haben Eigenwert $\lambda$ auf der Diagonale,
auf der oberen Nebendiagonale

Matrix-Potenzen $A = Q^{-1}JQ \Rightarrow A^n = Q^{-1}J^nQ$
$\vert\lambda_i\vert<1 \Leftrightarrow A^n \to 0$

Singulärwertzerlegung $U^\ast A V = \operatorname{diag}( s_1,s_2,\ldots)$ , , unitär
singuläre Werte $s_1\ge s_2\ge \cdots \ge s_k>0$ , $k=\operatorname{Rang} A$
sind Wurzeln der Eigenwerte von $A^\ast A$
Spalten von sind Eigenvektoren von $A^\ast A$
Spalten von sind Eigenvektoren von $AA^\ast$

(Autor: M. Reble)

[vorangehende Seite] [nachfolgende Seite]

[Gesamtverzeichnis][Seitenübersicht]

automatisch erstellt am 31.1.2006

Eigenwerte / -vektoren	$Av = \lambda v \,, \; v \neq 0 \Leftrightarrow \operatorname{det}(A-\lambda E) = 0$
	$\sum\lambda_i = \operatorname{Spur} A\,, \quad \prod\lambda_i = \operatorname{det} A$
	$A^{\operatorname t}$ hat Eigenwert $\lambda$ $A^{-1}$ hat Eigenvektor und Eigenwert $1/\lambda$ hat Eigenvektor und Eigenwert $\lambda^n$ $Q^{-1}AQ$ hat Eigenvektor $Q^{-1}v$ und Eigenwert $\lambda$
Diagonalisierung	für alle Eigenwerte: algebr. = geometr. Vielfachheit $B^{-1}AB = \operatorname{diag}(\lambda_1,\ldots,\lambda_n)$ $B = (b_1,\ldots,b_n)$ Basis aus Eigenvektoren
Jordan-Form	Blockdiagonalmatrix $J = B^{-1} A B = \operatorname{diag}(J_1,\ldots,J_m)$ Blöcke haben Eigenwert $\lambda$ auf der Diagonale, auf der oberen Nebendiagonale
Matrix-Potenzen	$A = Q^{-1}JQ \Rightarrow A^n = Q^{-1}J^nQ$ $\vert\lambda_i\vert<1 \Leftrightarrow A^n \to 0$
Singulärwertzerlegung	$U^\ast A V = \operatorname{diag}( s_1,s_2,\ldots)$ , , unitär singuläre Werte $s_1\ge s_2\ge \cdots \ge s_k>0$ , $k=\operatorname{Rang} A$ sind Wurzeln der Eigenwerte von $A^\ast A$ Spalten von sind Eigenvektoren von $A^\ast A$ Spalten von sind Eigenvektoren von $AA^\ast$