Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Formelsammlung - Lineare Algebra

Determinanten und lineare Gleichungssysteme

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Determinante $ \operatorname{det} A^{\operatorname t}= \operatorname{det} A\,, \quad \operatorname{det} (AB) = \operatorname{det} A \, \operatorname{det} B$

$ \operatorname{det} A^{-1} = \left(\operatorname{det} A\right)^{-1}\,, \quad \operatorname{det} A^{n} = \left(\operatorname{det} A\right)^{n}$

Vertauschung zweier Spalten (Zeilen) ändert Vorzeichen.

Addition eines Vielfachen einer Spalte (Zeile) zu einer anderen ändert den Wert der Determinante nicht.
   
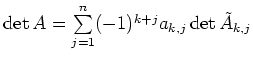Entwicklung $ \operatorname{det} A = \sum\limits_{j=1}^n (-1)^{k+j} a_{k,j} \operatorname{det} \tilde A_{k,j}$ (Entwicklung nach Zeile $ k$)

         $ = \sum\limits_{i=1}^n (-1)^{i+l} a_{i,l} \operatorname{det} \tilde A_{i,l}$ (Entwicklung nach Spalte $ l$)
   
$ \operatorname{det} A = 0$ $ \Leftrightarrow 0$ ist Eigenwert

$ \Leftrightarrow Ax=b$ hat keine eindeutige Lösung

$ \Leftrightarrow A$ hat nicht vollen Rang

$ \Leftrightarrow A$ ist nicht invertierbar
   
Lineare Gleichungssysteme besitzen entweder genau eine, keine oder unendlich viele Lösungen
   
Gauß-Transformationen Die Lösungsmenge eines LGS ändert sich nicht bei:

Vertauschen zweier Gleichungen

Multiplikation einer Gleichung mit $ r\neq 0$

Addition zweier Gleichungen
   
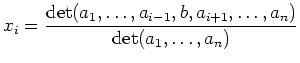Cramersche Regel $ \displaystyle x_i = \frac{\operatorname{det}(a_1,\ldots,a_{i-1},b,a_{i+1},\ldots,a_n)} {\operatorname{det}(a_1,\ldots,a_n)}$
   
Ausgleichsproblem $ \vert Ax-b\vert \to \min \Leftrightarrow A^{\operatorname t}Ax = A^{\operatorname t}b$
   
(Autor: M. Reble)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 31.1.2006