Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Formelsammlung - Analysis mehrerer Veränderlicher

Differentiation

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
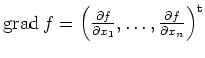Gradient $ \operatorname{grad} f = \left(\frac{\partial f}{\partial x_1},\ldots, \frac{\partial f}{\partial x_n}\right)^{\operatorname t}$
   
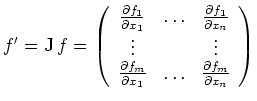Jacobi-Matrix $ f^\prime = \operatorname{J} f = \left( \begin{array}{ccc} \frac{\parti... ...tial x_1} & \ldots & \frac{\partial f_m}{\partial x_n} \end{array} \right) $
   
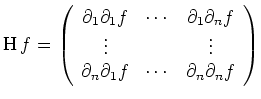Hesse-Matrix $ \operatorname{H}f = \left( \begin{array}{ccc} \partial_1\partial_1 f & \cdot... ... \partial_n\partial_1 f & \cdots & \partial_n\partial_n f \end{array}\right)$
   
Kettenregel $ h(x) = g(y), \; y = f(x): \quad h^\prime(x) = g^\prime(y)\,f^\prime(x)$
Taylor-Entwicklung $ f(x+h) = \sum_{\vert\alpha\vert\le n} \frac{1}{\alpha!} \partial^\alpha f(x) h^\alpha + R$

Restglied $ R = \sum_{\vert\alpha\vert=n+1} \frac{1}{\alpha!} \partial^\alpha f(x+\theta h) h^\alpha$ für ein $ \theta\in[0,1]$

Ordnung 2:

$ f(x+h) = f(x) + \left(\operatorname{grad}f(x)\right)^{\operatorname t}h + \frac{1}{2} h^t \operatorname{H}f (x) h + O(\vert h\vert^3) $
Tangential-Ebene Fläche $ f(x,y,z) = c$ bzw. $ (u,v) \mapsto p(u,v)$

Normalenvektor $ n = \operatorname{grad}f$ bzw. $ n = p_u \times p_v$
Richtungsableitung $ \partial_v f(x) = (\operatorname{grad} f)^{\operatorname t}v$
Implizite Funktionen $ \operatorname{det} f_x(x_*,y_*) \neq 0 \Rightarrow f(x,y)=0$ auflösbar nach $ x$
Umkehrfunktion $ f$ ist lokal umkehrbar, wenn $ \operatorname{det} f^\prime (x_0) \neq 0$

$ (f^{-1})^\prime (y) = (f^\prime(x))^{-1}\, , \; y =f(x) \quad$ für $ x \approx x_0$
kritische Punkte $ \operatorname{grad} f(x) = 0$

elliptisch: Alle Eigenwerte von $ H$ haben das gleiche Vorzeichen

         $ \rightarrow$ lokales Extremum

hyperbolisch: Es gibt Eigenwerte mit verschiedenem Vorzeichen

         $ \rightarrow$ Sattelpunkt

parabolisch: Mindestens ein Eigenwert ist Null, und alle anderen Eigenwerte haben das gleiche Vorzeichen.
Lagrange-Multiplikatoren Extremwert $ x_*$ unter Nebenbedingungen $ g_i(x) = 0$

$ \Rightarrow f^\prime(x_*) = \lambda^{\operatorname t}g^\prime(x_*)$
Kuhn-Tucker

Bedingung

 Extremwert $ x_*$ unter Nebenbedingungen $ g_i(x) \geq 0$

$ \Rightarrow f^\prime(x_*) = \lambda^{\operatorname t}g^\prime(x_*)\,,\quad \lambda^{\operatorname t} g(x_*) = 0$
  Minimum: $ \lambda_i \geq 0$, Maximum: $ \lambda_i \leq 0$
(Autor: M. Reble)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 31.1.2006