Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Formelsammlung - Komplexe Analysis

Integration

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Kurvenintegral $ \displaystyle\int\limits_C f \,dz = \int\limits_a^b f(z(t))\,z^\prime(t)\,dt\,,\quad C:\,t\mapsto z(t)\,, \ t\in[a,b]$
   
Stammfunktion $ f$ im Gebiet $ D$ komplex differenzierbar, $ C$ ein in $ D$ verlaufender Weg von $ z_0$ nach $ z_1$:

$ \displaystyle\int\limits_C f^\prime \, dz = f(z_1) - f(z_0) = \left[f\right]_{z_0}^{z_1}$
   
Singularitäten schwache Singularität: $ \lim\limits_{z \to a} (z-a) f(z) = 0$

Pol $ n$-ter Ordnung: $ \vert z-a\vert^{n-1}\vert f(z)\vert\to \infty$ für $ z\to a$, $ (z-a)^n f(z)$ beschränkt für $ z\to a$

wesentliche Singularität: $ (z-a)^n f(z)$ für kein $ n$ beschränkt
   
Cauchys Theorem $ f$ analytisch in $ D$ bis auf endlich viele schwache Singularitäten, $ C\subset D$ geschlossene Kurve, homotop zu einem Punkt:

$ \displaystyle\int\limits_C f(z) \,dz = 0$
   
Cauchysche Integralformel $ f$ analytisch, $ n(C,z)$ Umlaufzahl von $ C$ bzgl. $ z$:

$ \displaystyle n(C,z)f(z)=\frac{1}{2\pi\mathrm{i}}\int\limits_C \frac{f(w)}{w-z}\,dw$
   
Integralformel für

Ableitungen

 $ f$ analytisch, $ n(C,z)$ =1:

$ \displaystyle f^{(n)}(z) = \frac{n!}{2\pi\mathrm{i}}\int\limits_C\frac{f(w)}{(w-z)^{n+1}}\,dw$
   
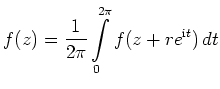Mittelwerteigenschaft $ \displaystyle f(z) = \frac{1}{2\pi}\int\limits_0^{2\pi} f(z+re^{\mathrm{i}t})\,dt$
   
Maximumprinzip $ \max\limits_{z \in D}\vert f(z)\vert \leq \max\limits_{z \in\, \partial D}\vert f(z)\vert$
   
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 31.1.2006