Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Formelsammlung - Fourier-Analysis

Fourier-Transformation

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
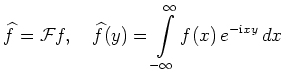 Fourier-Transformation $ \displaystyle \widehat{f}={\cal F}f,\quad \widehat{f}(y) = \int\limits_{-\infty}^{\infty} f(x)\,e^{-\mathrm{i}xy}\,dx $
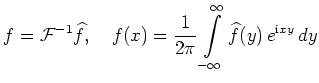 Inverse Fourier-Transformation $ \displaystyle f={\cal F}^{-1}\widehat{f},\quad f(x) = \frac{1}{2\pi}\int\limits_{-\infty}^{\infty}\widehat{f}(y) \,e^{\mathrm{i}xy}\,dy $
    
    

Transformationsregeln

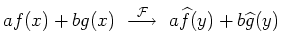 Linearität $ af(x) + bg(x) \ \stackrel{{\cal F}}{\longrightarrow} \ a\widehat{f}(y) + b\widehat{g}(y)$
    
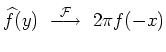 Symmetrie $ \widehat{f}(y) \ \stackrel{{\cal F}}{\longrightarrow} \ 2\pi f(-x)$
    
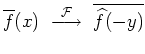 Konjugation $ \overline{f}(x) \ \stackrel{{\cal F}}{\longrightarrow} \ \overline{\widehat{f}(-y)}$

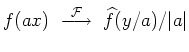 Skalierung $ f(ax) \ \stackrel{{\cal F}}{\longrightarrow} \ \widehat{f}(y/a) / \vert a\vert$
    
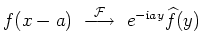 Verschiebung $ f(x-a) \ \stackrel{{\cal F}}{\longrightarrow} \ e^{-\mathrm{i}ay}\widehat{f}(y)$
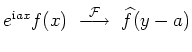   $ e^{\mathrm{i}ax}f(x) \ \stackrel{{\cal F}}{\longrightarrow} \ \widehat{f}(y-a)$
    
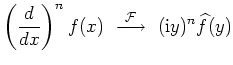 Differentiation $ \displaystyle\left(\frac{d}{dx}\right)^n f(x) \ \stackrel{{\cal F}}{\longrightarrow} \ (\mathrm{i}y)^n \widehat{f}(y)$
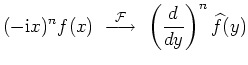   $ \displaystyle(-\mathrm{i}x)^n f(x)\ \stackrel{{\cal F}}{\longrightarrow} \ \left(\frac{d}{dy}\right)^n \widehat{f}(y)$
    
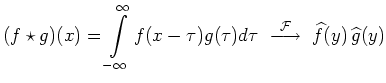 Faltung $ \displaystyle (f \star g)(x) = \int\limits_{-\infty}^{\infty}f(x-\tau)g(\tau)d\tau \ \stackrel{{\cal F}}{\longrightarrow} \ \widehat{f}(y)\,\widehat{g}(y)$
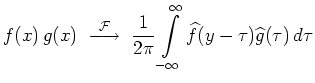   $ \displaystyle f(x)\,g(x) \ \stackrel{{\cal F}}{\longrightarrow} \ \frac{1}{2\pi}\int\limits_{-\infty}^{\infty} \widehat{f}(y-\tau)\widehat{g}(\tau) \,d\tau$
    
 Spezielle Funktionen  
  
$ f$ $ \widehat{f}$
$ 1$ $ 2\pi\delta(y)$
$ 1$   für $ x \in [-a, a]\,,\ 0\ $ sonst $ 2a \operatorname{sinc}(ay)$
$ \operatorname{sign}(x)$ $ 2/(\mathrm{i}y)$
$ e^{-a\vert x\vert}$ $ 2a/(a^2+y^2)$
$ e^{-ax^2}$ $ \sqrt{\pi/a}\,e^{-y^2/(4a)}$
    
    
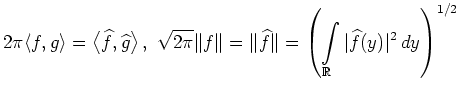 Satz von Plancherel $ \displaystyle 2\pi \langle f,g\rangle = \big\langle \widehat{f}, \widehat{g} ... ...Vert =\left(\int\limits_\mathbb{R} \vert\widehat{f}(y)\vert^2\,dy\right)^{1/2}$
    
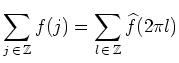 Poisson-Summationsformel $ \displaystyle \sum\limits_{j\, \in \, \mathbb{Z}} f(j) = \sum\limits_{l\, \in \, \mathbb{Z}} \widehat{f}(2\pi l)$
    
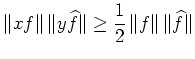 Heisenbergs Unschärfeprinzip $ \Vert x f\Vert \, \Vert y\widehat{f} \Vert \geq \dfrac{1}{2}\,\Vert f\Vert\,\Vert\widehat{f}\Vert$
    
 Rekonstruktionssatz Hat $ f$ Bandbreite $ h$, d.h. $ \widehat{f}(y)=0$ für $ \vert y\vert > h$, dann gilt

$ \displaystyle f(x) = \sum\limits_{j\,\in\,\mathbb{Z}} f(j\pi/h)\operatorname{sinc}(hx-j\pi) $.
    

(Autor: Marcus Reble)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 31.1.2006