Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Komplexe Analysis - Komplexe Funktionen - Konforme Abbildungen

Konforme Abbildung

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Eine auf dem Definitionsgebiet $ D$ injektive komplex differenzierbare Funktion $ z\mapsto w=f(z)$ bezeichnet man als konforme Abbildung.

Konforme Abbildungen sind isotrop und winkeltreu. Bezeichnet

$\displaystyle t \mapsto w(t) = f(z(t)) $

das Bild einer Kurve unter einer komplex differenzierbaren Abbildung $ f$, dann gilt für das Bild der Tangente in einem Punkt $ z_0=z(t_0)$

$\displaystyle w'(t_0) = f'(z_0)z'(t_0) \,. $

Unabhängig von der Wahl der Kurve $ z$ wird die Tangente in $ z_0$ um den Faktor $ \vert f'(z_0)\vert$ gestreckt und um den Winkel $ \operatorname{arg}(f'(z_0))$ gedreht. Insbesondere bleibt der Schnittwinkel zweier Kurven unter der Abbildung $ f$ erhalten. Konforme Abbildungen können damit zur Transformation orthogonaler Gitter verwendet werden.

Als Beispiel werden die Gerade

$\displaystyle C_1:\quad$ $\displaystyle z_1(t)=-2\mathrm{i}+t(1+\mathrm{i}),\quad t\in\mathbb{R}\,,$    

und der Kreis


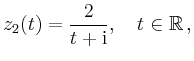$\displaystyle C_2:\quad$ $\displaystyle z_2(t)=\frac{2}{t+\mathrm{i}},\quad t\in\mathbb{R}\,,$    

sowie die Abbildung

$\displaystyle f(z)=z^2,\quad f'(z)=2z $

betrachtet.
\includegraphics[width=.8\linewidth]{Konform_Bild1}
Für $ t_0=1$ schneiden sich $ C_1$ und $ C_2$ im Punkt $ z_0=1-\mathrm{i}$, wobei

$\displaystyle z_1'(1)$ $\displaystyle = 1+\mathrm{i} = \sqrt{2} e^{\mathrm{i}\pi/4}$    

und


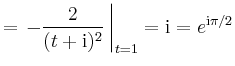$\displaystyle z_2'(1)$ $\displaystyle = \left.-\frac{2}{(t+\mathrm{i})^2}\,\right\vert _{t=1} = \mathrm{i} =e^{\mathrm{i}\pi/2}$    

ist, d.h. die Kurven schneiden sich in einem Winkel von $ \pi/4$.

Die Bilder $ f(C_1)$ und $ f(C_2)$ schneiden sich für $ t_0=1$ im Punkt $ z_0^2=(1-\mathrm{i})^2=-2\mathrm{i}$, wobei

$\displaystyle f'(1-\mathrm{i})z_1'(1) = 2(1-\mathrm{i})(1+\mathrm{i}) = 4$    

und


$\displaystyle f'(1-\mathrm{i})z_2'(1) = 2(1-\mathrm{i})\mathrm{i} = 2(\mathrm{i}+1) = 2\sqrt{2}e^{\mathrm{i}\pi/4}$    

ist, d.h. auch die Bildkurven schneiden sich in einem Winkel von $ \pi/4$. Der Streckungsfaktor beträgt

$\displaystyle \vert f'(1-\mathrm{i})\vert=2\sqrt{2}\,. $

Als Beispiel wird die Abbildung

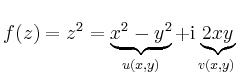
$\displaystyle f(z)=z^2=\underbrace{x^2-y^2}_{u(x,y)} + \mathrm{i}\underbrace{2xy}_{v(x,y)} $

betrachtet.

Das Gitter $ x=$const. bzw. $ y=$const. wird dabei auf zwei Scharen orthogonaler Parabeln

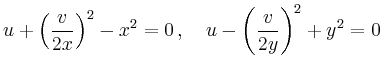
$\displaystyle u +\left(\frac{v}{2x}\right)^2-x^2 = 0\,,\quad u -\left(\frac{v}{2y}\right)^2 +y^2 = 0 $

abgebildet, wobei $ x$ und $ y$ Parameter sind.

\includegraphics[height=.4\moimagesize]{b_konform_1}   \includegraphics[height=.4\moimagesize]{b_konform_2}
$ xy$-Ebene   $ uv$-Ebene

Umgekehrt werden die zwei Scharen von orthogonalen Hyperbeln

$\displaystyle x^2-y^2 =$   const.$\displaystyle \,,\quad 2xy =$   const.

auf das Gitter $ u=$const. bzw. $ v=$const. abgebildet.

\includegraphics[height=.4\moimagesize]{b_konform_4}   \includegraphics[height=.4\moimagesize]{b_konform_3}
$ xy$-Ebene   $ uv$-Ebene
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 21.11.2013