Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Komplexe Analysis - Komplexe Funktionen - Konforme Abbildungen

Elementare konforme Abbildungen

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Durch $ w = e^z$ wird der Streifen

$\displaystyle z:\ 0< \operatorname{Im} z < \gamma $

mit $ \gamma \leq 2 \pi$ auf den Sektor

$\displaystyle w:\ 0 < \operatorname{arg} w < \gamma $

abgebildet.

\includegraphics[height=.3\moimagesize]{a_exponential_2}   \includegraphics[height=.3\moimagesize]{a_exponential_1}
$ z$-Ebene   $ w$-Ebene

Insbesondere erhält man für $ \gamma=2\pi$ als Bild die geschlitzte Ebene $ \mathbb{C}\backslash\mathbb{R}_0^+$.

Entsprechend kann man mit Hilfe des komplexen Logarithmus Sektoren konform auf Streifen abbilden.

Die Joukowski-Abbildung

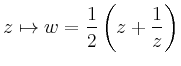
$\displaystyle z\mapsto w=\frac{1}{2}\left(z+\frac{1}{z}\right) $

bildet das Innere des Einheitskreises $ K:\, \vert z\vert<1$ konform auf das Komplement $ D=\mathbb{C} \backslash [-1,1]$ des Segments $ [-1,1]$ ab. Sie lässt sich schrittweise konstruieren. Zunächst wird $ K$ durch die Möbius-Transformation

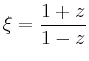
$\displaystyle \xi=\frac{1+z}{1-z} $

auf die Halbebene $ H:$ $ \operatorname{Re} z>0$ abgebildet. Durch Quadrieren,

$\displaystyle \eta=\xi^2\,, $

erhält man die geschlitzte Ebene $ \mathbb{C} \backslash \mathbb{R}_0^-$. Diese kann schließlich durch eine weitere Möbius-Transformation

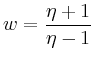
$\displaystyle w=\frac{\eta +1}{\eta -1} $

auf $ D$ abgebildet werden. Setzt man die drei Transformationen ineinander ein, so erhält man

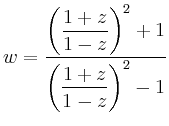
$\displaystyle w=\frac{\left(\displaystyle \frac{1+z}{1-z}\right)^2+1}{\left(\displaystyle \frac{1+z}{1-z} \right)^2-1} $

und nach Vereinfachung die behauptete Form von $ w$.
\includegraphics[height=.4\moimagesize]{b_joukowski_1}   \includegraphics[height=.4\moimagesize]{b_joukowski_2}
$ z$-Ebene   $ w$-Ebene
Die Bilder zeigen die Transformation des orthogonalen Gitters $ r=\vert z\vert=$const. und $ \varphi=\operatorname{arg}(z)=$const. unter dieser Abbildung.

Bildet man mit der Joukowski-Abbildung einen Kreis ab, dessen Mittelpunkt $ m$ in der oberen Halbebene liegt, der durch den Punkt $ z=1$ geht und außerdem $ z=-1$ einschließt, so erhält man als Bilder die sogenannten Joukowski-Profile, die in der Aerodynamik, z.B. bei Flugzeugtragflächen, eine Rolle spielen.

\includegraphics[height=.4\moimagesize]{Joukowski_Bild1}   \includegraphics[height=.4\moimagesize]{Joukowski_Bild2}
$ z$-Ebene   $ w$-Ebene
\includegraphics[height=.4\moimagesize]{Joukowski_Bild3}   \includegraphics[height=.4\moimagesize]{Joukowski_Bild4}
$ z$-Ebene   $ w$-Ebene

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 21.11.2013