Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Komplexe Analysis - Komplexe Integration - Kurvenintegrale

Komplexe Integranden

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Das Integral einer komplexwertigen Funktion

$\displaystyle f(t) = u(t)+\mathrm{i}v(t),\quad t\in[a,b] \,, $

ist durch

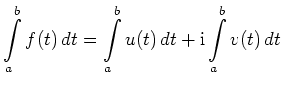
$\displaystyle \int\limits_a^b f(t)\,dt = \int\limits_a^b u(t)\,dt + \mathrm{i}\int\limits_a^b v(t)\,dt $

definiert. Es ist in der üblichen Weise linear und additiv. Darüber hinaus gilt

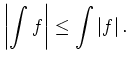
$\displaystyle \left\vert \int f\right\vert \le \int \vert f\vert \,. $

Für die Funktion $ f(t)=e^{\mathrm{i}t}$ ist der Wert des Integrals über das Intervall $ [0,\varphi]$

$\displaystyle \int\limits_0^\varphi e^{\mathrm{i}t} dt = \int\limits_0^\varphi ... ...s t\right]_0^\varphi = \sin \varphi +\mathrm{i}\left(1-\cos \varphi \right)\,. $

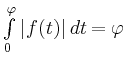Da $ \vert f\vert =1$ gilt, ist $ \int\limits_0^\varphi \vert f(t)\vert\,dt=\varphi$. Andererseits ist

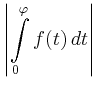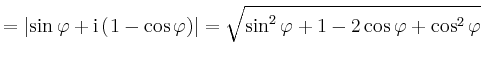$\displaystyle \left\vert\int\limits_0^\varphi f(t)\,dt \right\vert$ $\displaystyle =\left\vert\sin \varphi +\mathrm{i}\left(1-\cos \varphi \right)\right\vert = \sqrt{\sin^2 \varphi + 1 -2\cos \varphi +\cos^2\varphi}$    
  $\displaystyle = \sqrt{2-2\cos \varphi}\,.$    

Dies lässt sich mit Hilfe des Additionstheorems umformen zu

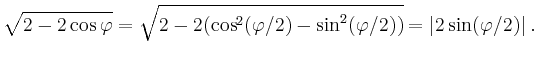
$\displaystyle \sqrt{2-2\cos \varphi} = \sqrt{2-2(\cos^2(\varphi/2)-\sin^2(\varphi/2))} = \vert 2\sin (\varphi/2)\vert\,. $

Aufgrund der geometrischen Definition der Sinusfunktion ist $ \vert\sin(t)\vert\leq \vert t\vert$, und man erkennt, dass die Betragsungleichung gilt.
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 21.11.2013