Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Komplexe Analysis - Komplexe Integration - Kurvenintegrale

Komplexes Kurvenintegral

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]

Für einen stetig differenzierbaren Weg

$\displaystyle C:\ t\mapsto z(t),\quad t\in [a,b] \,, $

in der komplexen Ebene bezeichnet man

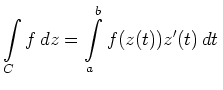
$\displaystyle \int\limits_C f\,dz = \int\limits_a^b f(z(t))z'(t)\,dt \, $

als komplexes Kurvenintegral. Die Definition ist bei gleichbleibender Orientierung unabhängig von der gewählten Parametrisierung des Weges $ C$. Bei Umkehrung der Durchlaufrichtung ändert sich das Vorzeichen des Integrals.

Wird die Kurve $ z(t)\,,\, t\in[a,b]$, durch eine stetig differenzierbare Abbildung $ t\mapsto s$ mit $ ds/dt >0$ umparametrisiert in $ \tilde{z}(s)\,,\,s\in[c,d]\,,$ so gilt für das Kurvenintegral über $ f$
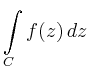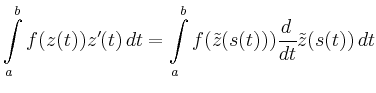$\displaystyle \int\limits_C f(z)\,dz$ $\displaystyle =$ $\displaystyle \int\limits_a^b f(z(t))z'(t)\,dt = \int\limits_a^b f(\tilde{z}(s(t)))\frac{d}{dt}\tilde{z}(s(t))\,dt$  
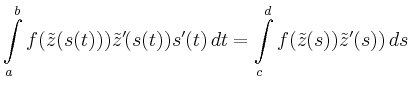  $\displaystyle =$ $\displaystyle \int\limits_a^b f(\tilde{z}(s(t)))\tilde{z}'(s(t))s'(t)\,dt = \int\limits_c^d f(\tilde{z}(s))\tilde{z}'(s))\,ds$  
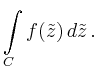  $\displaystyle =$ $\displaystyle \int\limits_C f(\tilde{z})\,d\tilde{z}\,.$  

Das Integral verändert sich also unter orientierungserhaltenden Umparametrisierungen nicht.
Das Integral von $ f(z)=z$ über der geradlinigen Verbindung

$\displaystyle C: z(t) = (1-t)p+tq\,,\quad t\in[0,1]\,, $

zweier Punkte $ p$ und $ q$ der komplexen Zahlenebene ist
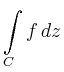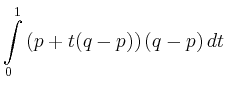$\displaystyle \int\limits_C f\,dz$ $\displaystyle =$ $\displaystyle \int\limits_0^1 \left(p+t(q-p)\right)(q-p)\,dt$  
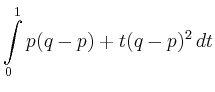  $\displaystyle =$ $\displaystyle \int\limits_0^1 p(q-p)+t(q-p)^2\,dt$  
  $\displaystyle =$ $\displaystyle pq-p^2+(q-p)^2/2 = q^2/2-p^2/2\,.$  

Für $ f(z)=1/z$ und den Kreis

$\displaystyle C:\ z(t)=re^{\mathrm{i}t}\,,\quad t\in[0,2\pi]\,, $

ergibt sich für das Kurvenintegral

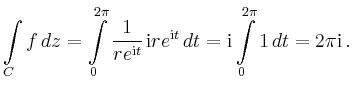
$\displaystyle \int\limits_Cf\,dz=\int\limits_0^{2\pi}\frac{1}{re^{\mathrm{i}t}}... ...m{i}re^{\mathrm{i}t}\,dt=\mathrm{i}\int\limits_0^{2\pi}1\,dt=2\pi\mathrm{i}\,. $

Dagegen erhält man für $ f(z)=z^n$, $ n \neq -1$,
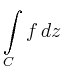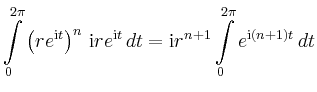$\displaystyle \int\limits_C f \, dz$ $\displaystyle =$ $\displaystyle \int\limits_0^{2 \pi} \left( r e^{\mathrm{i}t}\right)^n \,\mathrm... ...{i}t}\,dt = \mathrm{i} r^{n+1} \int\limits_0^{2 \pi} e^{\mathrm{i}(n+1)t} \, dt$  
  $\displaystyle =$ $\displaystyle \mathrm{i} r^{n+1} \left[ \frac{1}{\mathrm{i}(n+1)} e^{\mathrm{i}(n+1)t}\right]_0^{2 \pi} = 0 \,.$  

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 21.11.2013