Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Komplexe Analysis - Komplexe Integration - Kurvenintegrale

Eigenschaften des komplexen Kurvenintegrals

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Das komplexe Kurvenintegral ist linear bezüglich des Integranden, d.h.

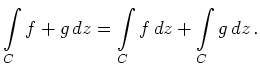
$\displaystyle \int\limits_C f+g\,dz = \int\limits_C f\,dz +\int\limits_C g\,dz \,. $

Darüber hinaus ist $ \int$ additiv bezüglich des Integrationsweges.

\includegraphics[width=.5\textwidth]{Kurvenintegral_Bild1}

Setzt sich ein (orientierter) Weg $ C$ aus zwei Wegen $ C_1$ und $ C_2$ zusammen, $ C = C_1 + C_2$, so gilt

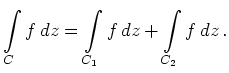
$\displaystyle \int\limits_C f\,dz = \int\limits_{C_1} f\,dz +\int\limits_{C_2} f\,dz \,. $

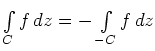Insbesondere ist $ \int\limits_C f\,dz = -\int\limits_{-C}f\,dz$, wobei $ -C$ den in entgegengesetzter Richtung durchlaufenen Weg $ C$ bezeichnet.
Das Kurvenintegral der Funktion $ f(z)=\sqrt{z}$ entlang des skizzierten Weges

\includegraphics[width=.3\textwidth]{Wurzel_z_Bild1}

besteht aus drei Komponenten:

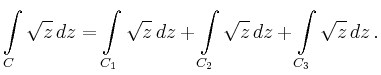
$\displaystyle \int\limits_C \sqrt{z}\,dz= \int\limits_{C_1} \sqrt{z}\,dz+ \int\limits_{C_2} \sqrt{z}\,dz+ \int\limits_{C_3} \sqrt{z}\,dz\,. $

Diese Integrale werden nun separat berechnet.

Für $ C_1$: $ t\mapsto z(t)=t$, $ 0 \leq t \leq 1$, folgt wegen $ \frac{dz}{dt}=1$

$\displaystyle \int\limits_0^1 \sqrt{t}\,dt=\left[\frac{2}{3}t^{3/2}\right]_0^1=\frac{2}{3}\,. $

Für $ C_2$: $ t\mapsto z(t)=e^{\mathrm{i}t}$, $ 0 \leq t \leq \frac{\pi}{2}$, folgt wegen $ \frac{dz}{dt}=\mathrm{i}e^{\mathrm{i}t}$
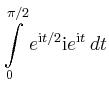$\displaystyle \int\limits_0^{\pi/2} e^{\mathrm{i}t/2}\mathrm{i}e^{\mathrm{i}t}\,dt$ $\displaystyle =$ $\displaystyle \int\limits_0^{\pi/2} \mathrm{i}e^{3\mathrm{i}t/2}=\left[\frac{2}... ...mathrm{i}t/2}\right]_0^{\pi/2} = \frac{2}{3}e^{3\mathrm{i}\pi/4}-\frac{2}{3}\,.$  

Für $ C_3$: $ t\mapsto z(t)=\mathrm{i}-t\mathrm{i}$, $ 0 \leq t \leq 1$, folgt wegen $ \frac{dz}{dt}=-\mathrm{i}$
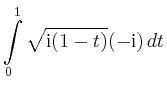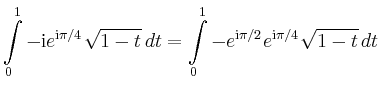$\displaystyle \int\limits_0^{1} \sqrt{\mathrm{i}(1-t)}(-\mathrm{i})\,dt$ $\displaystyle =$ $\displaystyle \int\limits_0^{1} -\mathrm{i}e^{\mathrm{i}\pi/4}\sqrt{1-t}\,dt= \int\limits_0^1 -e^{\mathrm{i}\pi/2}e^{\mathrm{i}\pi/4}\sqrt{1-t}\,dt$  
  $\displaystyle =$ $\displaystyle \left[\frac{2}{3}e^{3\mathrm{i}\pi/4}(1-t)^{3/2}\right]_0^{1}=-\frac{2}{3}e^{3\mathrm{i}\pi/4}\,.$  

Für das gesamte Kurvenintegral erhält man also
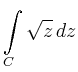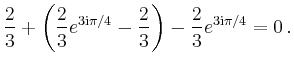$\displaystyle \int\limits_C \sqrt{z}\,dz$ $\displaystyle =$ $\displaystyle \frac{2}{3}+\left(\frac{2}{3}e^{3\mathrm{i}\pi/4}-\frac{2}{3}\right) -\frac{2}{3}e^{3\mathrm{i}\pi/4}=0\,.$  

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 21.11.2013