Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Komplexe Analysis - Komplexe Integration - Fundamentale Sätze

Singularitäten

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Ist eine komplexe Funktion $ f$ in der Umgebung $ D\backslash a$ eines Punktes $ a$ analytisch, so lässt sich der Typ der Definitionslücke wie folgt klassifizieren.

Man beachte, dass die Klassifizierung nicht auf Funktionen wie $ \operatorname{Ln}(z-a)$ oder $ \sqrt{z-a}$ anwendbar ist, da in keinem Kreisring um $ a$ eine konsistente stetige Definition möglich ist.

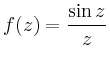
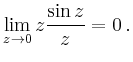
Die Funktion

$\displaystyle f(z)=\frac{\sin z}{z} $

besitzt bei $ a=0$ eine schwache Singularität, denn

$\displaystyle \lim_{z\to 0}z\frac{\sin z}{z}=0\,. $

Die Funktion

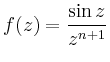
$\displaystyle f(z)=\frac{\sin z}{z^{n+1}} $

besitzt bei $ a=0$ einen Pol $ n$-ter Ordnung, denn

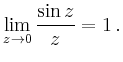
$\displaystyle \lim_{z\to 0}\frac{\sin z}{z}=1\,. $

Damit folgt $ \lim\limits_{z\to 0}z^nf(z)=1$ und $ z^kf(z)\to\infty$ für $ k<n$ und $ z\to 0$.

Die Funktion

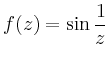
$\displaystyle f(z)=\sin\frac{1}{z} $

besitzt bei $ a=0$ eine wesentliche Singularität, denn mit $ z=\frac{1}{\mathrm{i}t}$ ist

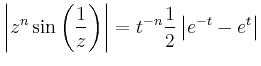
$\displaystyle \left\vert z^n\sin\left(\frac{1}{z}\right)\right\vert = t^{-n}\frac{1}{2}\left\vert e^{-t}-e^t\right\vert $

unbeschränkt für $ t\to\infty$ und alle $ n\in\mathbb{N}$.

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 21.11.2013