Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Komplexe Analysis - Komplexe Integration - Residuenkalkül

Berechnung von Residuen

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Hat $ f$ eine einfache Polstelle bei $ a$, so ist

$\displaystyle \underset{a}{\operatorname{Res}}f = \lim_{z\to a} (z-a) f(z) \,. $

Für eine Polstelle $ n$-ter Ordnung gilt

$\displaystyle \underset{a}{\operatorname{Res}}f = \lim_{z\to a} \frac{1}{(n-1)!} \left[\left(\frac{d}{dz}\right)^{n-1} ((z-a)^n f(z))\right] \,. $

Bei einer einfachen Polstelle lässt sich $ f$ in der Form

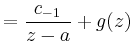$\displaystyle f(z)$ $\displaystyle =\frac{c_{-1}}{z-a}+g(z)$    

schreiben, wobei $ g$ in einer Umgebung von $ a$ analytisch ist. Somit gilt


$\displaystyle \lim_{z\to a} (z-a) f(z)$ $\displaystyle = \lim_{z\to a}\left(c_{-1}+(z-a)g(z)\right) =c_{-1}\,.$    

Für eine Polstelle $ n$-ter Ordnung gilt analog

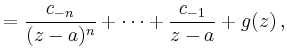$\displaystyle f(z)$ $\displaystyle =\frac{c_{-n}}{(z-a)^n}+\cdots+\frac{c_{-1}}{z-a}+g(z)\,,$    

wobei $ g$ in einer Umgebung von $ a$ analytisch ist. Somit gilt


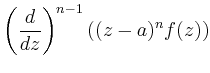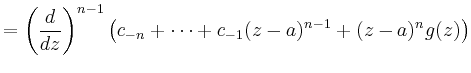$\displaystyle \left(\frac{d}{dz}\right)^{n-1} ((z-a)^n f(z))$ $\displaystyle = \left(\frac{d}{dz}\right)^{n-1} \left(c_{-n}+\cdots +c_{-1}(z-a)^{n-1} +(z-a)^ng(z)\right)$    
  $\displaystyle \to(n-1)!\,c_{-1}$    

für $ z\to a$.

Die Funktion

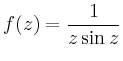
$\displaystyle f(z)=\frac{1}{z\sin z} $

hat eine Polstelle zweiter Ordnung bei $ z=0$ und Polstellen erster Ordnung bei $ z=k\pi$, $ k\in\mathbb{Z}\backslash\{0\}$. Für die Residuen erhält man

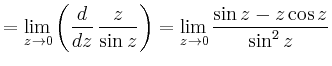$\displaystyle \underset{0}{\operatorname{Res}}f$ $\displaystyle =\lim_{z\to0}\left(\frac{d}{dz}\,\frac{z}{\sin z}\right) = \lim_{z\to0}\frac{\sin z-z\cos z}{\sin^2 z}$    
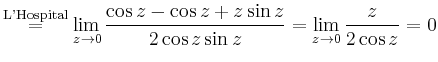  $\displaystyle \overset{\text{L'Hospital}}{=} \lim_{z\to0}\frac{\cos z -\cos z +z\sin z}{2\cos z\sin z} = \lim_{z\to0}\frac{z}{2\cos z}=0$    

und


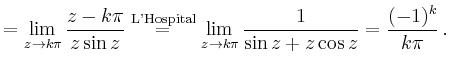$\displaystyle \underset{k\pi}{\operatorname{Res}}f$ $\displaystyle = \lim_{z\to k\pi}\frac{z-k\pi}{z\sin z} \overset{\text{L'Hospital}}{=} \lim_{z\to k\pi}\frac{1}{\sin z+z\cos z} = \frac{(-1)^k}{k\pi}\,.$    

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 21.11.2013