Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Komplexe Analysis - Komplexe Funktionen - Grundfunktionen

Möbius-Transformation

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]

Eine rationale Funktion mit Zähler- und Nennergrad $ \le 1$,

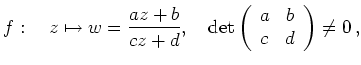
$\displaystyle f:\quad z \mapsto w = \frac{az + b}{cz + d},\quad \operatorname{det} \left(\begin{array}{cc} a&b \\ c&d \end{array}\right)\neq 0 \,, $

wird als Möbius-Transformation oder gebrochen lineare Transformation bezeichnet. Dabei dürfen $ z$ und $ w$ Werte in $ \bar{\mathbb{C}} = \mathbb{C}\cup\{\infty\}$ annehmen.

Die Umkehrabbildung ist

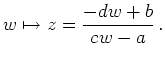
$\displaystyle w \mapsto z = \frac{-dw + b}{cw - a}\,. $

Eine Möbius-Transformation ist durch die Bilder $ w_j$ von drei Punkten $ z_j$ eindeutig bestimmt und kann mit Hilfe des Doppelverhältnisses in der Form

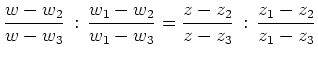
$\displaystyle \frac{w-w_2}{w-w_3}\,:\,\frac{w_1-w_2}{w_1-w_3} = \frac{z-z_2}{z-z_3}\,:\,\frac{z_1-z_2}{z_1-z_3} $

angegeben werden. Diese Identität kann nach $ z$ oder $ w$ aufgelöst werden, wobei die Konvention $ \frac{\infty}{\infty} = 1$ zu verwenden ist.
Die Möbius-Transformation, die $ 1$ auf 0, 0 auf $ 1$ und $ \mathrm{i}$ auf $ \infty$ abbildet, erhält man über das Doppelverhältnis

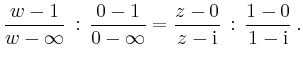
$\displaystyle \frac{w-1}{w-\infty}\,:\,\frac{0-1}{0-\infty} = \frac{z-0}{z-\mathrm{i}}\,:\,\frac{1-0}{1-\mathrm{i}}\,. $

Dies entspricht

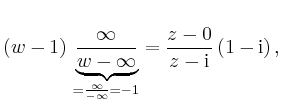
$\displaystyle (w-1)\,\underbrace{\frac{\infty}{w-\infty}}_{=\frac{\infty}{-\infty}=-1} = \frac{z-0}{z-\mathrm{i}}\,(1-\mathrm{i})\,, $

und damit ist

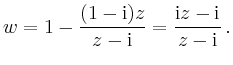
$\displaystyle w=1-\frac{(1-\mathrm{i})z}{z-\mathrm{i}}=\frac{\mathrm{i}z-\mathrm{i}}{z-\mathrm{i}}\,. $

Eine andere Möglichkeit ist, die Punkte einzeln in die Funktionsgleichung einzusetzen und das entstehende unterbestimmte Gleichungssystem für $ a,b,c,d$ zu lösen:

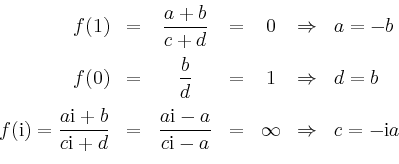
\begin{displaymath} \begin{array}{rcccccl} f(1)&=&\displaystyle \frac{a+b}{c+d}&... ...{c\text{i}-a} &=&\infty &\Rightarrow &c=-\text{i}a \end{array}\end{displaymath}

Mit $ a=\mathrm{i}$ ergibt sich die oben angegebene Form für $ f$.

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 21.11.2013