Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Komplexe Analysis - Komplexe Integration - Residuenkalkül

Rationale Integranden

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Für eine rationale Funktion $ f$ ohne reelle Polstellen und mit Zählergrad um mindestens $ 2$ kleiner als der Nennergrad gilt

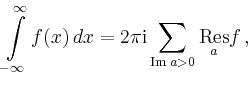
$\displaystyle \int\limits_{-\infty}^\infty f(x)\,dx = 2\pi\mathrm{i} \sum_{\operatorname{Im} a>0} \underset{a}{\operatorname{Res}} f \,, $

wobei die Residuen an allen Polstellen in der oberen Halbebene summiert werden.

Alternativ kann man über die Polstellen in der unteren Halbebene summieren. Dabei ändert sich aufgrund der entgegengesetzten Orientierung das Vorzeichen der Summe. Dies zeigt insbesondere, dass die Summe aller Residuen von $ f$ null ist.

\includegraphics[width=.4\linewidth]{e_rationale}

Ist $ C=C_1+C_2$ ein Halbkreis wie in obiger Skizze, wobei $ r$ so groß gewählt wird, dass alle Polstellen $ a$ von $ f$ mit $ \operatorname{Im} a > 0$ im Inneren liegen, so gilt nach dem Residuensatz

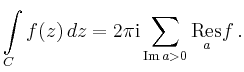
$\displaystyle \int\limits_C f(z)\,dz =2\pi\mathrm{i}\sum_{\operatorname{Im}a>0} \underset{a}{\operatorname{Res}} f\,. $

Weiterhin ist

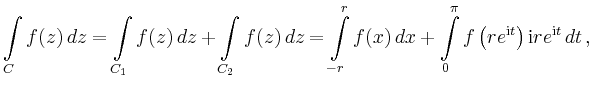
$\displaystyle \int\limits_C f(z)\,dz =\int\limits_{C_1} f(z)\,dz+\int\limits_{C... ...t\limits_0^\pi f\left(re^{\mathrm{i}t}\right)\mathrm{i}re^{\mathrm{i}t}\,dt\,, $

wobei $ C_2$ mit

$\displaystyle C_2: \quad z(t)=re^{\mathrm{i}t},\quad 0\le t\le\pi\,, $

parametrisiert wurde. Da $ f$ eine rationale Funktion mit Zählergrad um mindestens 2 kleiner als der Nennergrad ist, gibt es eine Konstante $ M>0$, so dass

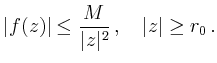
$\displaystyle \vert f(z)\vert\le \frac{M}{\vert z\vert^2}\,, \quad \vert z\vert\ge r_0\,. $

Folglich verschwindet das letzte Integral für $ r\to\infty$, während das vorletzte gegen

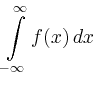
$\displaystyle \int\limits_{-\infty}^\infty f(x)\,dx $

konvergiert.
Als Beispiel wird die Funktion

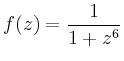
$\displaystyle f(z)=\frac{1}{1+z^6} $

betrachtet. Die Funktion besitzt die $ 6$ einfachen Polstellen

$\displaystyle a_j=e^{\mathrm{i}(\pi/6+2\pi j/6)},\quad j=0,\ldots,5\,, $

wobei $ a_0$, $ a_1$, $ a_2$ in der oberen Halbebene liegen. Man erhält

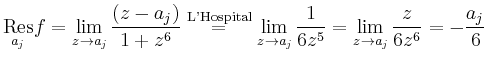
$\displaystyle \underset{a_j}{\operatorname{Res}}f = \lim_{z\to a_j} \frac{(z-a_... ...im_{z\to a_j} \frac{1}{6z^5}= \lim_{z\to a_j} \frac{z}{6z^6} = -\frac{a_j}{6} $

und damit

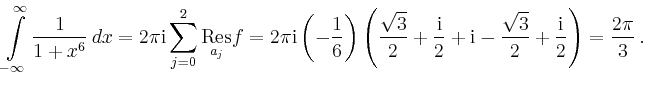
$\displaystyle \int\limits_{-\infty}^{\infty} \frac{1}{1+x^6}\,dx = 2\pi\mathrm{... ...thrm{i} - \frac{\sqrt{3}}{2}+\frac{\mathrm{i}}{2}\right) = \frac{2\pi}{3}\,. $

Als Beispiel wird die Funktion

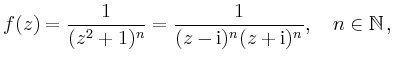
$\displaystyle f(z)=\frac{1}{(z^2+1)^n}=\frac{1}{(z-\mathrm{i})^n(z+\mathrm{i})^n},\quad n\in\mathbb{N}\,, $

betrachtet. Nur die $ n$-fache Polstelle $ a=\mathrm{i}$ liegt in der oberen Halbebene, und man erhält

$\displaystyle \underset{\mathrm{i}}{\operatorname{Res}}f$ $\displaystyle = \frac{1}{(n-1)!}\left[\left(\frac{d}{dz}\right)^{n-1} \left((z-\mathrm{i})^nf(z)\right) \right]_{z=\mathrm{i}}$    
  $\displaystyle = \frac{1}{(n-1)!} \left[\frac{(-n)(-n-1)\cdots(-2n+2)}{(z+\mathrm{i})^{2n-1}} \right]_{z=\mathrm{i}}$    
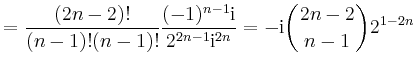  $\displaystyle =\frac{(2n-2)!}{(n-1)!(n-1)!} \frac{(-1)^{n-1}\mathrm{i}}{2^{2n-1}\mathrm{i}^{2n}}= -\mathrm{i}\binom{2n-2}{n-1}2^{1-2n}$    

und damit

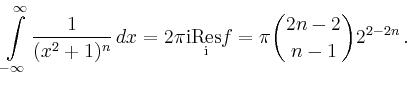
$\displaystyle \int\limits_{-\infty}^{\infty} \frac{1}{(x^2+1)^n}\,dx = 2\pi\mat... ...}\underset{\mathrm{i}}{\operatorname{Res}}f = \pi\binom{2n-2}{n-1}2^{2-2n}\,. $

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 21.11.2013