Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Komplexe Analysis - Komplexe Integration - Residuenkalkül

Transzendente Integranden

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Für eine rationale Funktion $ f$ ohne reelle Polstellen und mit Zählergrad kleiner als der Nennergrad gilt

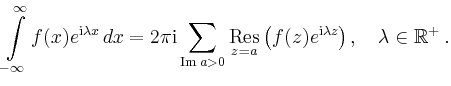
$\displaystyle \int\limits_{-\infty}^\infty f(x)e^{\mathrm{i}\lambda x}\,dx = 2\... ...}}\left(f(z)e^{\mathrm{i}\lambda z}\right), \quad \lambda \in \mathbb{R}^+ \,. $

Für $ \lambda<0$ wird entsprechend die negative Summe aller Residuen in der unteren Halbebene gebildet.

\includegraphics[width=.4\linewidth]{e_transzendente}

Berandet $ C=C_1+C_2+C_3+C_4$ ein Rechteck wie in obiger Skizze, wobei $ c$ so groß gewählt wird, dass alle Polstellen $ a$ von $ fe^{\mathrm{i}\lambda\cdot}$ mit $ \operatorname{Im} a>0$ im Inneren liegen, so gilt nach dem Residuensatz

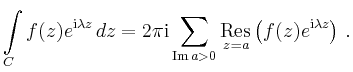
$\displaystyle \int\limits_C f(z)e^{\mathrm{i}\lambda z}\,dz =2\pi\mathrm{i}\sum... ... \underset{z=a}{\operatorname{Res}}\left(f(z)e^{\mathrm{i}\lambda z}\right)\,. $

Weiterhin ist

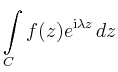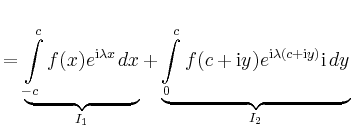$\displaystyle \int\limits_C f(z)e^{\mathrm{i}\lambda z}\,dz$ $\displaystyle = \underbrace{\int\limits_{-c}^c f(x)e^{\mathrm{i}\lambda x} \,dx... ..._0^c f(c+\mathrm{i}y)e^{\mathrm{i}\lambda(c+\mathrm{i}y)} \mathrm{i}\,dy}_{I_2}$    
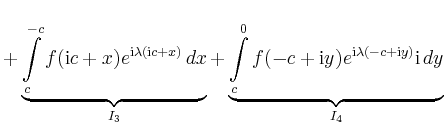  $\displaystyle + \underbrace{\int\limits_c^{-c} f(\mathrm{i}c+x)e^{\mathrm{i}\la... ...c^0 f(-c+\mathrm{i}y)e^{\mathrm{i}\lambda(-c+\mathrm{i}y)}\mathrm{i}\,dy}_{I_4}$    

mit geeigneten Parametrisierungen der $ C_j$. Da $ f$ eine rationale Funktion mit Zählergrad kleiner als der Nennergrad ist, gibt es eine Konstante $ M>0$, so dass

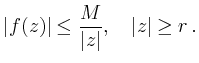
$\displaystyle \vert f(z)\vert\le \frac{M}{\vert z\vert},\quad \vert z\vert\ge r\,. $

Für $ c>r$ lässt sich damit $ I_2$ durch

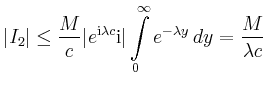
$\displaystyle \vert I_2\vert \le \frac{M}{c}\vert e^{\mathrm{i}\lambda c}\mathrm{i}\vert\int\limits_0^\infty e^{-\lambda y}\,dy = \frac{M}{\lambda c} $

abschätzen, d.h. $ \lim\limits_{c\to\infty} I_2 =0$. Entsprechend verfährt man für $ I_4$. Für $ I_3$ erhält man

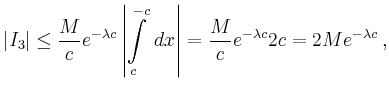
$\displaystyle \vert I_3\vert \le \frac{M}{c}e^{-\lambda c}\left\vert\int\limits_c^{-c}\,dx\right\vert =\frac{M}{c}e^{-\lambda c}2c=2Me^{-\lambda c}\,, $

d.h. $ \lim\limits_{c\to\infty} I_3=0 $ und insgesamt

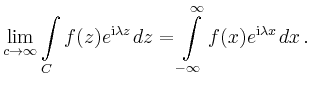
$\displaystyle \lim_{c\to\infty} \int\limits_C f(z)e^{\mathrm{i}\lambda z}\,dz = \int\limits_{-\infty}^{\infty}f(x)e^{\mathrm{i}\lambda x }\,dx\,. $

Als Beispiel wird das Integral

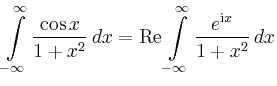
$\displaystyle \int\limits_{-\infty}^\infty \frac{\cos x}{1+x^2}\,dx =\operatorname{Re} \int\limits_{-\infty}^\infty \frac{e^{\mathrm{i}x}}{1+x^2}\,dx $

betrachtet. Der Integrand hat zwei einfache Polstellen bei $ a_1=\mathrm{i}$ und $ a_2=-\mathrm{i}$, wobei nur die Polstelle $ a_1$ in der oberen Halbebene liegt. Für das Residuum bei $ a_1=\mathrm{i}$ erhält man

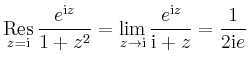
$\displaystyle \underset{z=\mathrm{i}}{\operatorname{Res}}\,\frac{e^{\mathrm{i}z... ..._{z\to\mathrm{i}} \frac{e^{\mathrm{i}z}}{\mathrm{i}+z} =\frac{1}{2\mathrm{i}e} $

und damit

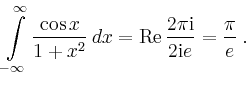
$\displaystyle \int\limits_{-\infty}^\infty \frac{\cos x}{1+x^2}\,dx=\operatorname{Re} \frac{2\pi\mathrm{i}}{2\mathrm{i}e} = \frac{\pi}{e}\,. $

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 21.11.2013