Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Komplexe Analysis - Potenzreihen - Laurent-Reihe

Laurent-Reihe

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Eine in einem Kreisring

$\displaystyle D:\ r_1 < \vert z-a\vert < r_2 $

analytische Funktion $ f$ kann in eine Laurent-Reihe

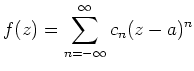
$\displaystyle f(z) = \sum_{n=-\infty}^\infty c_n (z-a)^n $

entwickelt werden, die in $ D$ absolut konvergiert. Die Koeffizienten besitzen die Integraldarstellung

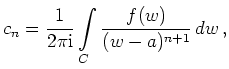
$\displaystyle c_n = \frac{1}{2\pi\mathrm{i}} \int\limits_C \frac{f(w)}{(w-a)^{n+1}}\,dw \,, $

wobei $ C\subset D$ ein beliebiger entgegen dem Uhrzeigersinn durchlaufener Kreis um $ a$ ist.

Die Laurent-Reihe entspricht einer Zerlegung

$\displaystyle f(z) = f_1(z-a) + f_2(1/(z-a)) $

von $ f$ in zwei analytische Funktionen $ f_j$, die bis auf eine Konstante eindeutig bestimmt sind. Die Konvergenzgebiete von $ f_1$ und $ f_2$ sind offene Kreisscheiben um $ a$ mit Radius $ r_2$ bzw. $ 1/r_1$.
Zur Vereinfachung wird der Entwicklungspunkt $ a$ in den Ursprung verschoben ($ a=0$). Nun wählt man, wie in der Abbildung skizziert, zwei Kreise, die den Punkt $ z$ einschließen.

\includegraphics[width=.4\linewidth]{e_laurentreihe}

Dann gilt nach der Cauchyschen Integralformel

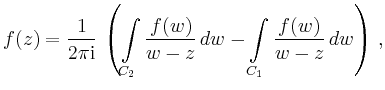
$\displaystyle f(z) = \frac{1}{2\pi\mathrm{i}}\, \left( \int\limits_{C_2} \frac{f(w)}{w-z}\,dw - \int\limits_{C_1} \frac{f(w)}{w-z}\,dw \right) \,, $

wobei das Minuszeichen die Orientierung von $ C_1$ umkehrt; $ C_2-C_1$ ist der orientierte Rand eines Kreisrings, der $ z$ enthält.

In dem ersten Integral ersetzt man $ 1/(w-z)$ durch

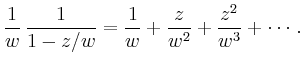
$\displaystyle \frac{1}{w}\,\frac{1}{1-z/w} = \frac{1}{w} + \frac{z}{w^2} + \frac{z^2}{w^3} + \cdots \,. $

Da $ \vert z\vert<\vert w\vert$ für $ w\in C_2$, ist diese geometrische Reihe absolut konvergent. Im zweiten Integral ist $ \vert z\vert>\vert w\vert$, und man verwendet die Entwicklung

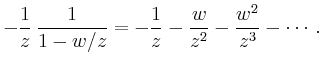
$\displaystyle -\frac{1}{z}\,\frac{1}{1-w/z} = -\frac{1}{z}-\frac{w}{z^2}-\frac{w^2}{z^3}-\cdots\,. $

Man kann also die beiden Integrale durch die Summen

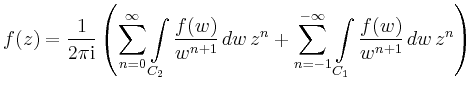
$\displaystyle f(z)=\frac{1}{2\pi\mathrm{i}}\left(\sum_{n=0}^\infty \int\limits_... ...\sum_{n=-1}^{-\infty} \int\limits_{C_1} \frac{f(w)}{w^{n+1}}\,dw\, z^n \right) $

darstellen.

Berücksichtigt man, dass sich der Integrationsweg für die auf $ D$ analytische Funktion $ f(w)/w^{n+1}$ verschieben lässt, so ergibt sich die angegebene Formel für die Koeffizienten.

Das obige Argument zeigt ebenfalls die Aufspaltung in die zwei analytischen Funktionen $ f_j$. Deren Eindeutigkeit folgt aus der Eindeutigkeit der Laurent-Entwicklung. Ihre Koeffizienten sind durch die Integralformel gegeben.

Als Beispiel werden verschiedene Laurent-Entwicklungen der Funktion

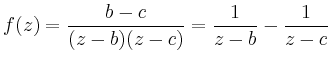
$\displaystyle f(z) =\frac{b-c}{(z-b)(z-c)}=\frac{1}{z-b}-\frac{1}{z-c} $

mit $ \vert b\vert<\vert c\vert$ um den Entwicklungspunkt $ a=0$ betrachtet.

\includegraphics[width=.3\moimagesize]{Laurent_Bild1}   \includegraphics[width=.3\moimagesize]{Laurent_Bild2}   \includegraphics[width=.3\moimagesize]{Laurent_Bild3}
$ \vert z\vert<\vert b\vert\qquad\ $   $ \vert b\vert<\vert z\vert<\vert c\vert\qquad$   $ \vert c\vert<\vert z\vert\qquad\ $

(i)
$ \left\vert z \right\vert< \left\vert b \right\vert $: Mit Hilfe der geometrischen Reihe erhält man

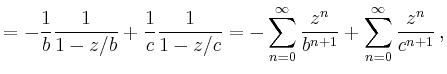$\displaystyle f(z)$ $\displaystyle =-\frac{1}{b}\frac{1}{1-z/b}+\frac{1}{c}\frac{1}{1-z/c} = -\sum_{n=0}^\infty \frac{z^n}{b^{n+1}} + \sum_{n=0}^\infty \frac{z^n}{c^{n+1}}\,,$    

wobei die erste Reihe für $ \vert z\vert<\vert b\vert$ und die zweite Reihe für $ \vert z\vert<\vert c\vert$ konvergiert. Damit entspricht für $ \vert z\vert<\vert b\vert$ die Laurent-Reihe der Taylor-Reihe


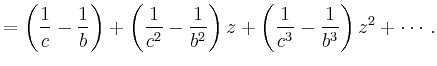$\displaystyle f(z)$ $\displaystyle =\left(\frac{1}{c}-\frac{1}{b}\right) +\left(\frac{1}{c^2}-\frac{1}{b^2}\right)z +\left(\frac{1}{c^3}-\frac{1}{b^3}\right)z^2+\cdots\,.$    

(ii)
$ \left\vert b \right\vert <\left\vert z \right\vert< \left\vert c \right\vert$: Schreibt man

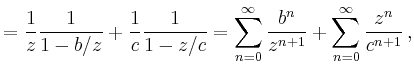$\displaystyle f(z)$ $\displaystyle =\frac{1}{z}\frac{1}{1-b/z}+\frac{1}{c}\frac{1}{1-z/c}= \sum_{n=0}^\infty \frac{b^n}{z^{n+1}} +\sum_{n=0}^\infty \frac{z^n}{c^{n+1}}\,,$    

so konvergiert die erste Reihe für $ \vert b\vert<\vert z\vert$ und die zweite für $ \vert z\vert<\vert c\vert$. Daraus erhält man für $ \vert b\vert<\vert z\vert<\vert c\vert$ für $ f$ die Laurent-Reihe


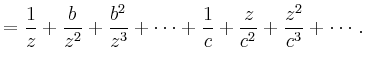$\displaystyle f(z)$ $\displaystyle =\frac{1}{z}+\frac{b}{z^2}+\frac{b^2}{z^3}+\cdots +\frac{1}{c}+\frac{z}{c^2}+\frac{z^2}{c^3}+\cdots\,.$    

(iii)
$ \vert c\vert<\vert z\vert$: Analog ergibt sich schließlich

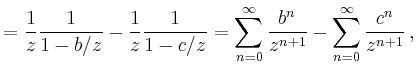$\displaystyle f(z)$ $\displaystyle =\frac{1}{z}\frac{1}{1-b/z}-\frac{1}{z}\frac{1}{1-c/z} =\sum_{n=0}^\infty \frac{b^n}{z^{n+1}}- \sum_{n=0}^\infty \frac{c^n}{z^{n+1}}\,,$    

wobei die erste Reihe für $ \vert b\vert<\vert z\vert$ und die zweite für $ \vert c\vert<\vert z\vert$ konvergiert. Damit gilt für die Laurent-Reihe von $ f$ um $ a=0$ für $ \vert c\vert<\vert z\vert$


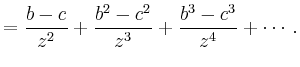$\displaystyle f(z)$ $\displaystyle =\frac{b-c}{z^2}+\frac{b^2-c^2}{z^3}+\frac{b^3-c^3}{z^4}+\cdots\,.$    

Ist die Laurent-Reihe

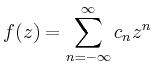
$\displaystyle f(z) = \sum\limits_{n = -\infty}^\infty c_n z^n $

für $ \left\vert z \right\vert =1$ konvergent, so erhält man mit $ z=e^{\mathrm{i}t}$ die Fourier-Reihe

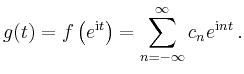
$\displaystyle g(t) = f \left( e^{\mathrm{i}t} \right) = \sum\limits_{n = -\infty}^\infty c_n e^{\mathrm{i} n t} \,. $

Die Berechnung der Koeffizienten kann entweder über das Kurvenintegral

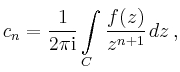
$\displaystyle c_n = \frac{1}{2 \pi \mathrm{i}} \int\limits_C \frac{f(z)}{z^{n+1}} \, dz \,, $

wobei $ C$ der positiv orientierte Einheitskreis ist, oder als trigonometrisches Integral

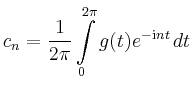
$\displaystyle c_n = \frac{1}{2 \pi} \int\limits_0^{2 \pi} g(t) e^{- \mathrm{i} n t} \, dt $

erfolgen $ \left( dz = \mathrm{i} z\, dt\right)$.

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 21.11.2013