Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Komplexe Analysis - Potenzreihen - Differentialgleichungen

Regulärer Punkt einer komplexen Differentialgleichung

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Die Differentialgleichung

$\displaystyle r(z) u''(z) + q(z) u'(z) + p(z) u(z) = 0 $

ist bei $ z=a$ regulär, wenn $ q/r$ und $ p/r$ in einer Umgebung von $ a$ analytisch sind.

In einem regulären Punkt $ a$ exisitiert zu beliebigen Werten $ u(a)=u_0$, $ u'(a)=u_1$ eine eindeutige, in einer Umgebung von $ a$ analytische Lösung $ u$.
Insbesondere existieren zwei linear unabhängige Lösungen zu den Werten

$\displaystyle u(a)=0,\quad u'(a)=1 $

und

$\displaystyle u(a) =1 ,\quad u'(a)=0\, . $

Nach Division durch $ r$ kann man $ r=1$ annehmen und o. B. d. A. $ a=0$ setzen, d.h. man hat die Entwicklungen

$\displaystyle p(z) = p_0 + p_1 z + \cdots,\quad q(z) = q_0 + q_1 z + \cdots \,, $

mit $ \vert p_j\vert,\vert q_j\vert\le c s^j$ für ein $ s>0$. Der formale Ansatz

$\displaystyle u(z) = u_0 + u_1 z + \cdots +u_n z^n+\cdots\,,\quad u'(z) = u_1 +2u_2z +z + \cdots $

führt nach Koeffizientenvergleich der Entwicklungen

$\displaystyle p(z)u(z) =$ $\displaystyle \; p_0u_0+(p_1u_0+p_0u_1)z+\cdots+(p_nu_0+\cdots+p_0u_n)z^n+\cdots,$    
$\displaystyle q(z)u'(z) =$ $\displaystyle \;q_0u_1+(q_1u_1+2q_0u_2)z + \cdots$    
  $\displaystyle + (q_nu_1+2q_{n-1}u_2+\cdots+(n+1)q_0u_{n+1})z^n+\cdots,$    
$\displaystyle u''(z) =$ $\displaystyle \; 2 u_2+6u_3z+\cdots+(n+2)(n+1)u_{n+2}z^n+\cdots$    

auf die Rekursion


$\displaystyle 2u_2 =$ $\displaystyle -q_0u_1-p_0u_0\,,$    
$\displaystyle 6u_3 =$ $\displaystyle -(q_1u_1+2q_0u_2)-(p_1u_0+p_0u_1)\,,$    
$\displaystyle \vdots$      
$\displaystyle (n+2)(n+1)u_{n+2} =$ $\displaystyle -(q_nu_1+\cdots+(n+1)q_0u_{n+1}) - (p_nu_0+\cdots+p_0u_n)\,,$    
$\displaystyle \vdots$ $\displaystyle .$    

Man kann also alle Koeffizienten sukzessive aus $ u_0=u(0)$ und $ u_1=u'(0)$ berechnen. Dies zeigt insbesondere die Eindeutigkeit.

Es bleibt zu überprüfen, ob die Prozedur tatsächlich auf eine analytische Funktion führt. Dazu wird induktiv gezeigt, dass

$\displaystyle \vert u_j\vert \le d t^j $

mit noch zu wählenden positiven Konstanten $ d$ und $ t$ ist. Durch den Induktionsanfang ergibt sich für $ d$

$\displaystyle d\ge \vert u_0\vert$    und $\displaystyle \quad d \ge \vert u_1\vert/t\,. $

Für den Induktionsschritt erhält man aus der Rekursion

$\displaystyle \vert u_{n+2}\vert \le \frac{1}{(n+1)(n+2)}cd\left(s^nt^1+\cdots+(n+1)s^0t^{n+1} + s^nt^0+\cdots+s^0t^n\right)\,. $

Mit $ t\ge s$ und $ 1+\cdots+(n+1)=(n+1)(n+2)/2$ ergibt sich

$\displaystyle \vert u_{n+2}\vert \le cd\left(\frac{t^{n+1}}{2}+\frac{t^n}{(n+2)}\right) \le cd\left(\frac{1}{2t}+\frac{1}{t^2}\right)t^{n+2}\,. $

Dieser Ausdruck ist kleiner als $ d t^{n+2}$, wenn $ t$ so groß gewählt wird, dass

$\displaystyle c\left(\frac{1}{2t}+\frac{1}{t^2}\right)\le 1 $

gilt.

Auf diese Weise erhält man unter Umständen einen zu kleinen Konvergenzradius. Es kann gezeigt werden, dass $ t$ mit dem Minimum der Konvergenzradien von $ p$ und $ q$ übereinstimmt.

Wie die folgenden Beispiele zeigen, ist der Typ der Punkte meist unmittelbar aus der Form der Koeffizienten ersichtlich.

(i)
Für die Legendre-Differentialgleichung

$\displaystyle (1-z^2)u''(z)-2zu'(z)+\alpha(\alpha+1)u(z)=0 $

ist

$\displaystyle (q/r)(z) = -\frac{2z}{1-z^2}\,, \quad (p/r)(z) = \frac{\alpha(\alpha+1)}{1-z^2}\,, $

d.h. die Differentialgleichung ist in allen Punkten außer $ z=\pm1$ regulär.

(ii)
Für die Bessel-Differentialgleichung

$\displaystyle z^2u''(z)+zu'(z)+(z^2-\alpha^2)u(z)=0 $

ist

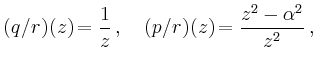
$\displaystyle (q/r)(z) = \frac{1}{z}\,, \quad (p/r)(z) = \frac{z^2-\alpha^2}{z^2}\,, $

d.h. die Differentialgleichung ist in allen Punkten außer $ z=0$ regulär.

Für die Legendre-Differentialgleichung

$\displaystyle (1-z^2)u''(z)-2zu'(z)+\alpha(\alpha+1)u(z)=0 $

ergibt sich mit dem Ansatz

$\displaystyle u(z) =u_0+u_1z+\cdots $

für die Koeffizienten von $ z^n$

$\displaystyle (n+2)(n+1)u_{n+2}-n(n-1)u_n-2nu_n+\alpha(\alpha+1)u_n=0 $

bzw.

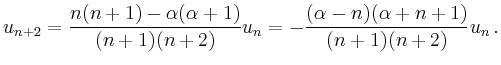
$\displaystyle u_{n+2}=\frac{n(n+1)-\alpha(\alpha+1)}{(n+1)(n+2)}u_n =-\frac{(\alpha-n)(\alpha+n+1)}{(n+1)(n+2)}u_n\,. $

Für die Anfangsbedingungen $ u(0)=1$ und $ u'(0)=0$ verschwinden alle ungeraden Koeffizienten, und man erhält

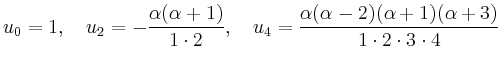
$\displaystyle u_0=1,\quad u_2=-\frac{\alpha(\alpha+1)}{1\cdot2},\quad u_4=\frac{\alpha(\alpha-2)(\alpha+1)(\alpha+3)}{1\cdot2\cdot3\cdot4} $

bzw. allgemein

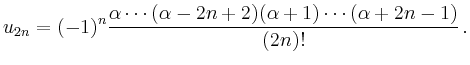
$\displaystyle u_{2n}=(-1)^n \frac{\alpha\cdots(\alpha-2n+2)(\alpha+1)\cdots(\alpha+2n-1)}{(2n)!}\,. $

Falls $ \alpha\ge 0 $ und gerade ist, bzw. falls $ \alpha < 0$ und ungerade ist, ist die Lösung

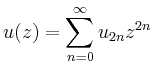
$\displaystyle u(z)=\sum_{n=0}^\infty u_{2n}z^{2n} $

ein Polynom. Die ersten geraden sogenannten Legendre-Polynome sind

$\displaystyle \alpha=0\;($oder $\displaystyle \alpha=-1)$ $\displaystyle \rightarrow u(z)=1$    
$\displaystyle \alpha=2\;($oder $\displaystyle \alpha=-3)$ $\displaystyle \rightarrow u(z)=1-3z^2$    
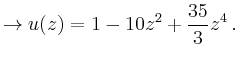$\displaystyle \alpha=4\;($oder $\displaystyle \alpha=-5)$ $\displaystyle \rightarrow u(z)=1-10z^2+\frac{35}{3}z^4\,.$    

Für die Anfangsbedingungen $ u(0)=0$ und $ u'(0)=1$ ergibt sich

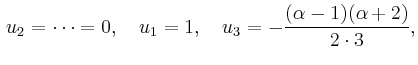$\displaystyle u_0=$ $\displaystyle \,u_2=\cdots=0,\quad u_1=1,\quad u_3=-\frac{(\alpha-1)(\alpha+2)}{2\cdot3},$    
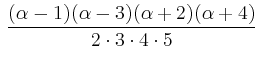$\displaystyle u_5=$ $\displaystyle \,\frac{(\alpha-1)(\alpha-3)(\alpha+2)(\alpha+4)}{2\cdot3\cdot4\cdot5}$    

bzw. allgemein

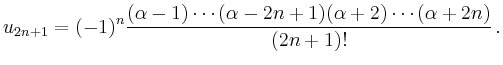
$\displaystyle u_{2n+1}=(-1)^n \frac{(\alpha-1)\cdots(\alpha-2n+1)(\alpha+2)\cdots(\alpha+2n)}{(2n+1)!}\,. $

Falls $ \alpha >0$ und ungerade ist, bzw. falls $ \alpha < 0$ und gerade ist, ist die Lösung

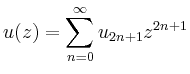
$\displaystyle u(z)=\sum_{n=0}^\infty u_{2n+1}z^{2n+1} $

ein Polynom. Die ersten ungeraden Legendre-Polynome sind

$\displaystyle \alpha=1\;($oder $\displaystyle \alpha=-2)$ $\displaystyle \rightarrow u(z)=z$    
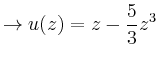$\displaystyle \alpha=3\;($oder $\displaystyle \alpha=-4)$ $\displaystyle \rightarrow u(z)=z-\frac{5}{3}z^3$    
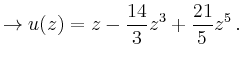$\displaystyle \alpha=5\;($oder $\displaystyle \alpha=-6)$ $\displaystyle \rightarrow u(z)=z-\frac{14}{3}z^3+\frac{21}{5}z^5\,.$    

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 21.11.2013