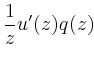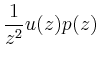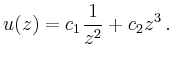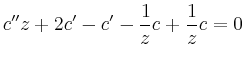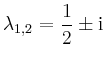Die Differentialgleichung
hat bei 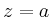 einen regulären singulären Punkt,
wenn
einen regulären singulären Punkt,
wenn 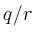 einen Pol höchstens
erster und
einen Pol höchstens
erster und 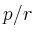 einen Pol
höchstens zweiter Ordnung bei
einen Pol
höchstens zweiter Ordnung bei 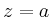 haben.
haben.
In einem regulären singulären Punkt 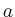 wird das
Verhalten der Lösungen
wird das
Verhalten der Lösungen 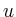 durch die charakteristische Gleichung
durch die charakteristische Gleichung
bestimmt, wobei 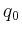 und
und 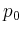 die führenden Koeffizienten von
die führenden Koeffizienten von 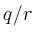 bzw.
bzw. 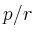 sind,
d.h,
sind,
d.h,
Ist die Differenz der Nullstellen
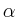 ,
, 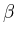 von
von 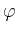 nicht ganzzahlig,
so existieren zwei linear unabhängige Lösungen
nicht ganzzahlig,
so existieren zwei linear unabhängige Lösungen
wobei 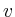 und
und 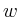 in einer Umgebung von
in einer Umgebung von 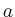 analytische Funktionen
mit
analytische Funktionen
mit
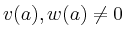 sind.
sind.
Sonst existiert im Allgemeinen nur eine Lösung dieses
Typs zu dem Exponenten 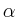 mit dem größten
Realteil.
Eine zweite Lösung kann dann durch Variation der
Konstanten, d.h. mit dem Ansatz
mit dem größten
Realteil.
Eine zweite Lösung kann dann durch Variation der
Konstanten, d.h. mit dem Ansatz
bestimmt werden.
Zur formalen Rechtfertigung des Lösungstyps
wird o. B. d. A. 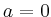 sowie
sowie 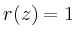 angenommen, und die Entwicklung
angenommen, und die Entwicklung
in die Differentialgleichung substituiert.
Der Vergleich des Koeffizienten von
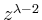 bei den Termen
bei den Termen
führt auf
d.h. nicht triviale Lösungen
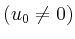 können nur
für Nullstellen von
können nur
für Nullstellen von 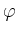 existieren.
Der Vergleich der Koeffizienten von
existieren.
Der Vergleich der Koeffizienten von
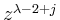 führt auf die Rekursion
führt auf die Rekursion
mit
Die Koeffizienten sind also sukzessive bestimmbar,
falls
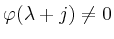 für alle
für alle 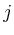 .
Da
.
Da 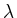 eine Nullstelle von
eine Nullstelle von 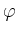 ist,
ist dies nur dann nicht der Fall, wenn
ist,
ist dies nur dann nicht der Fall, wenn
mit 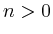 ist.
ist.
Die Euler-Differentialgleichung
besitzt bei 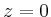 einen regulären singulären
Punkt und lässt sich durch den Ansatz
einen regulären singulären
Punkt und lässt sich durch den Ansatz
lösen.
Man erhält nach Einsetzen in die Differentialgleichung die charakteristische
Gleichung
für den Exponenten 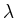 .
Die folgenden Beispiele illustrieren drei
qualitativ verschiedene Fälle:
.
Die folgenden Beispiele illustrieren drei
qualitativ verschiedene Fälle:
- (i)
- verschiedene Exponenten
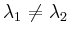 : Beispielsweise
erhält man für
: Beispielsweise
erhält man für 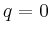 und
und
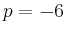
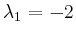
und
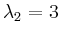
und damit die Lösung
- (ii)
- ein Exponent
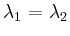 : Beispielsweise erhält man
für
: Beispielsweise erhält man
für 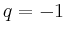 und
und 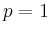 den Exponenten
den Exponenten
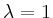 , d.h.
, d.h.
Eine zweite Lösung kann durch Variation der Konstanten bestimmt werden. Aus
folgt
bzw.
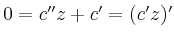 mit der Lösung
mit der Lösung
- (iii)
- komplex konjugierte Exponenten: Beispielsweise erhält man für
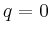 und
und
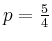
mit der Lösung
Eine reelle Lösung für reelles 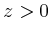 lässt sich mit Hilfe der Formel von
Euler-Moivre konstruieren:
lässt sich mit Hilfe der Formel von
Euler-Moivre konstruieren:
Mit
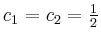 bzw.
bzw.
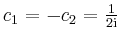 erhält man die linear
unabhängigen Lösungen
erhält man die linear
unabhängigen Lösungen
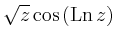
und
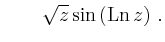
| |
automatisch erstellt
am 21.11.2013 |


![]() wird das
Verhalten der Lösungen
wird das
Verhalten der Lösungen ![]() durch die charakteristische Gleichung
durch die charakteristische Gleichung
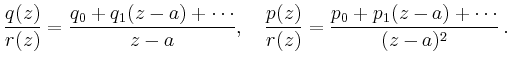
![]() ,
, ![]() von
von ![]() nicht ganzzahlig,
so existieren zwei linear unabhängige Lösungen
nicht ganzzahlig,
so existieren zwei linear unabhängige Lösungen
![]() mit dem größten
Realteil.
Eine zweite Lösung kann dann durch Variation der
Konstanten, d.h. mit dem Ansatz
mit dem größten
Realteil.
Eine zweite Lösung kann dann durch Variation der
Konstanten, d.h. mit dem Ansatz