Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Komplexe Analysis - Potenzreihen - Differentialgleichungen

Bessel-Differentialgleichung

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Die Bessel-Differentialgleichung

$\displaystyle z^2u''(z)+zu'(z)+(z^2-\alpha^2)u(z)=0 $

besitzt für $ \alpha \notin \mathbb{Z}$ die als Bessel-Funktion bezeichneten, linear unabhängigen Lösungen

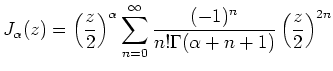
$\displaystyle J_{ \alpha}(z) = \left( \frac{z}{2} \right)^\alpha \sum_{n=0}^\infty \frac{(-1)^n}{n! \Gamma(\alpha +n+1)} \left( \frac{z}{2} \right)^{2n} $

und

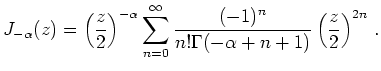
$\displaystyle J_{- \alpha}(z) = \left( \frac{z}{2} \right)^{-\alpha} \sum_{n=0}... ...ty \frac{(-1)^n}{n! \Gamma(-\alpha +n+1)} \left( \frac{z}{2} \right)^{2n}\,. $

Für $ \alpha \in \mathbb{Z} $ existiert eine Lösung mit der angegebenen Reihendarstellung nur für den positiven Index. Die zweite linear unabhängige Lösung ist in diesem Fall eine sogenannte Bessel-Funktion zweiter Art.

Einige spezielle Bessel-Funktionen sind

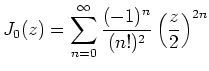
$\displaystyle J_0(z) = \sum_{n=0}^\infty \frac{(-1)^n}{(n!)^2} \left( \frac{z}{2} \right)^{2n} $

und

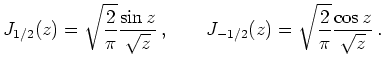
$\displaystyle J_{1/2}(z) =\sqrt{\frac{2}{\pi}} \frac{\sin z}{\sqrt{z}}\,, \qquad J_{-1/2}(z) =\sqrt{\frac{2}{\pi}} \frac{\cos z}{\sqrt{z}}\,. $

Die Bessel-Differentialgleichung hat bei $ z=0$ einen regulären singulären Punkt mit der charakteristischen Gleichung

$\displaystyle \lambda(\lambda-1)+\lambda-\alpha^2=\lambda^2-\alpha^2 =0 $

und damit $ \lambda =\pm \alpha$ als Exponenten. Mit dem Ansatz

$\displaystyle u(z)=z^\lambda(u_0+u_1z+\cdots) $

ergibt sich nach Koeffizientenvergleich die Rekursion

$\displaystyle \left(\left(\lambda+n\right)^2-\alpha^2\right)u_n+u_{n-2}=0 \,. $

Für den positiven Exponenten $ \lambda = \alpha \geq 0$ erhält man

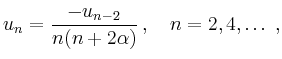
$\displaystyle u_n = \frac{-u_{n-2}}{n(n+2\alpha)} \,,\quad n= 2,4,\ldots \,, $

d.h.

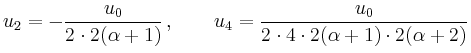
$\displaystyle u_2 = -\frac{u_0}{2 \cdot 2 (\alpha+1)} \,, \qquad u_4 = \frac{u_0}{2 \cdot 4 \cdot 2 (\alpha+1)\cdot 2 (\alpha+2)} $

und allgemein

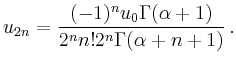
$\displaystyle u_{2n} = \frac{(-1)^n u_0\Gamma(\alpha+1)}{2^n n! 2^n \Gamma(\alpha+n+1)} \,. $

Mit $ u_{2n+1}=0$ und

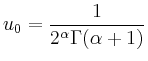
$\displaystyle u_0 = \frac{1}{2^\alpha \Gamma(\alpha+1)} $

folgt die behauptete Reihenentwicklung.

Für den negativen Exponenten $ \lambda = -\alpha \leq 0$ erhält man

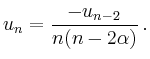
$\displaystyle u_n = \frac{-u_{n-2}}{n(n-2\alpha)} \,. $

Damit diese Rekursion für alle geraden $ n$ anwendbar ist, muss $ \alpha \notin \mathbb{N}$ vorausgesetzt werden. In diesem Fall erhält man dann völlig analog

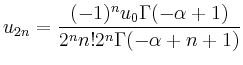
$\displaystyle u_{2n} = \frac{(-1)^n u_0\Gamma(-\alpha+1)}{2^n n! 2^n \Gamma(-\alpha+n+1)} $

und damit die Reihenentwicklung für die Lösung mit negativem Exponenten.

Die speziellen Darstellungen ergeben sich unmittelbar aus den Definitionen. Beispielsweise ist

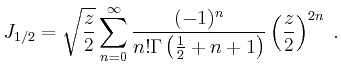
$\displaystyle J_{1/2}= \sqrt{\frac{z}{2}} \sum_{n=0}^\infty \frac{(-1)^n}{n! \Gamma \left( \frac{1}{2} +n +1 \right)} \left( \frac{z}{2} \right)^{2n} \;. $

Berücksichtigt man

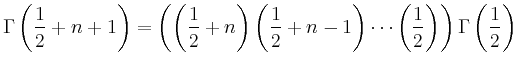
$\displaystyle \Gamma \left( \frac{1}{2} +n+1 \right) = \left( \left( \frac{1}{2... ...) \cdots \left( \frac{1}{2} \right) \right) \Gamma \left( \frac{1}{2}\right) $

sowie $ \Gamma \left( \frac{1}{2}\right) = \sqrt{\pi}$ und

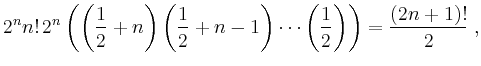
$\displaystyle 2^n n!\, 2^n \left( \left( \frac{1}{2} + n \right) \left( \frac{... ...-1 \right) \cdots \left( \frac{1}{2} \right) \right) = \frac{(2n+1)!}{2} \;, $

so ergibt sich

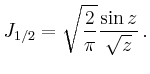
$\displaystyle J_{1/2}= \sqrt{\frac{2}{\pi}} \frac{\sin z}{\sqrt{z}} \,. $

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 21.11.2013