Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Partielle Differentialgleichungen - Klassifikation

Separationsansatz

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Für eine partielle Differentialgleichung der Form

$\displaystyle L_xu(x,y)=L_yu(x,y) $

mit $ L_x$ ($ L_y$) einem Differentialoperator, der nur auf die $ x$- ($ y$-) Variable wirkt, können spezielle Lösungen mit Hilfe des Ansatzes

$\displaystyle u(x,y)=v(x)w(y) $

konstruiert werden. Durch die Produktform werden die Variablen getrennt:

$\displaystyle (L_xv)w=v(L_yw)\quad\Leftrightarrow\quad\frac{L_xv(x)}{v(x)}=\frac{L_yw(y)}{w(y)} $

für $ u\neq0$. Da man in den Quotienten die Variablen $ x$ und $ y$ unabhängig voneinander variieren kann, müssen beide Quotienten konstant sein. Bezeichnet man diese sogenannte Separationskonstante mit $ \lambda$, so erhält man die Eigenwertprobleme

$\displaystyle L_xv=\lambda v\ ,\quad L_yw=\lambda w\,. $

Analog kann man für lineare partielle Differentialgleichungen in mehr als zwei Variablen vorgehen.
(Autor: Kimmerle)
Für die Wellengleichung

$\displaystyle u_{tt}(x,t)=c^2u_{xx}(x,t) $

liefert der Separationsansatz $ u(x,t)=v(x)w(t)$

$\displaystyle w^{\prime\prime}=\lambda w\ ,\quad c^2v^{\prime\prime}=\lambda v\,. $

Je nach Vorzeichen von $ \lambda\in\mathbb{R}$ sind mehrere Fälle zu unterscheiden.
(i)
$ \lambda=\varrho^2>0$ :

$\displaystyle w=c_1e^{\varrho t}+c_2e^{-\varrho t}\ ,\quad v=d_1e^{(\varrho/c)x}+d_2e^{-(\varrho/c)x} $

(ii)
$ \lambda=0$ :

$\displaystyle w=c_1+c_2t\ ,\quad v=d_1+d_2x $

(iii)
$ \lambda=-\varrho^2<0$ :

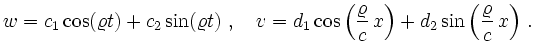
$\displaystyle w=c_1\cos(\varrho t)+c_2\sin(\varrho t)\ ,\quad v=d_1\cos\left(\frac{\varrho}{c}\,x\right)+d_2\sin\left(\frac{\varrho}{c}\,x\right)\,. $

Durch Einsetzen verifiziert man, dass die so konstruierten Lösungen tatsächlich die Wellengleichung erfüllen.
(Autor: Kimmerle)
Für die elliptische Differentialgleichung

$\displaystyle u_{xx}+u_{yy}+2u_y-u=0 $

führt der Separationsansatz

$\displaystyle u(x,y)=v(x)w(y) $

auf

$\displaystyle v^{\prime\prime}w+vw^{\prime\prime}-2vw^\prime-vw=0\,. $

Schließt man die triviale Lösung $ u=0$ aus, so folgt nach Division durch $ vw$

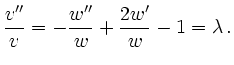
$\displaystyle \frac{v^{\prime\prime}}{v}=-\frac{w^{\prime\prime}}{w}+\frac{2w^\prime}{w}-1=\lambda\,. $

Je nach Vorzeichen der Separationskonstanten $ \lambda$ sind mehrere Fälle zu unterscheiden. Für zusätzlich gestellte Randbedingungen

$\displaystyle u(0,y)=u(\pi,y)=0\quad\Rightarrow\quad v(0)=v(\pi)=0 $

ergibt sich folgendes. Nur für $ \lambda=-n^2<0$ existieren nichttriviale Lösungen

$\displaystyle v(x)=c\sin(nx)\ ,\quad n\in\mathbb{N}\,. $

Damit folgt

$\displaystyle w^{\prime\prime}-2w^\prime+(1-n^2)w=0 $

mit der allgemeinen Lösung

$\displaystyle w(y)=d_1e^{(1+n)y}+d_2e^{(1-n)y}\,. $

(Autor: Kimmerle)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.5.2011