
Mathematik-Online-Kurs: Partielle Differentialgleichungen - Partielle Differentialgleichungen erster Ordnung

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Kurs: Partielle Differentialgleichungen - Partielle Differentialgleichungen erster Ordnung | |
Charakteristiken einer linearen partiellen Differentialgleichung erster Ordnung |
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
mit stetig differenzierbaren Funktionen
definierten Kurven
der linearen gewöhnlichen Differentialgleichung
d.h. sie kann aus einem Anfangswert
Ist sowohl ![]() als auch
als auch ![]() gleich 0
,
so ist die Lösung entlang der Charakteristiken
konstant.
Es muß dann nur das System gewöhnlicher
Differentialgleichungen für
gleich 0
,
so ist die Lösung entlang der Charakteristiken
konstant.
Es muß dann nur das System gewöhnlicher
Differentialgleichungen für ![]() gelöst
werden.
gelöst
werden.
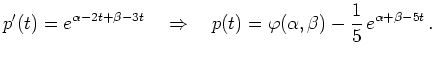
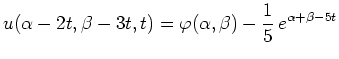
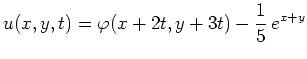
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
| automatisch erstellt am 5.5.2011 |