Graphen

Im folgenden eine Aufstellung der Graphen aller irreduziblen komplexen Spiegelungsgruppen mit den zugehörigen "Graden". Die Graphen sind aus [M. Broué, G. Malle, R. Rouquier, "On complex reflection groups and their associated Braid groups", CMS Conference Proceedings, 16, (1995), 1-13] übernommen.

Zunächst soll die Schreibweise anhand einiger Beispiele erläutert werden:

Knoten stehen für Elemente, die Zahl in den Knoten gibt die Elementordnung an, zum Beispiel entspricht $\epsfig{file=../Diagramme/Bobbel.eps}$ dem Element s mit s^d = 1.

Für Elementordnung d = 2 schreibt man eine leeren Knoten $\epsfig{file=../Diagramme/LeererBobbel.eps}$ .

Kanten symbolisieren die Relationen zwischen den Knoten :

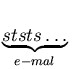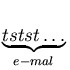$\epsfig{file=../Diagramme/Knochen.eps}$ entspricht der Präsentation s^c = t^d = 1 und $\underbrace{ststs \hdots}_{e-mal}^{}\,$ = $\underbrace{tstst \hdots}_{e-mal}^{}\,$ .

Dabei gibt es für spezielle Werte von e folgende Konventionen:

Bei e = 2 läßt man die Kante einfach weg:
$\epsfig{file=../Diagramme/KnochenOhne.eps}$ entspricht der Relation st = ts.
Beim häufig autretenden Wert e = 3 zeichnet man eine einfache Kante ohne Zahl:
$\epsfig{file=../Diagramme/KnochenEinfach.eps}$ entspricht der Relation sts = tst.
Bei e = 4 zeichnet man eine Doppelkante $\epsfig{file=../Diagramme/KnochenZwei.eps}$
und bei e = 6 eine Dreifachkante $\epsfig{file=../Diagramme/KnochenDrei.eps}$ .

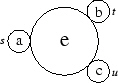Der Graph $\epsfig{file=../Diagramme/KreisBsp.eps}$ entspricht der Präsentation

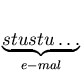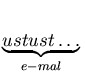s^a = t^b = u^c = 1 und $\underbrace{stustu \hdots}_{e-mal}^{}\,$ = $\underbrace{tustus \hdots}_{e-mal}^{}\,$ = $\underbrace{ustust \hdots}_{e-mal}^{}\,$ .

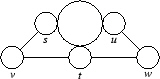Der Graph $\epsfig{file=../Diagramme/G31.eps}$ entspricht der Präsentation

s² = t² = u² = v² = w² = 1, uv = vu, sw = ws, vw = wv, sut = uts = tsu, svs = vsv, tvt = vtv, twt = wtw, wuw = uwu.

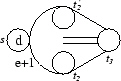Der Graph $\epsfig{file=../Diagramme/Bsp1.eps}$ entspricht der Präsentation

s^d = t'₂² = t₂² = t₃² = 1, st₃ = t₃s, st'₂t₂ = t'₂t₂s, t'₂t₃t'₂ = t₃t'₂t₃, t₂t₃t₂ = t₃t₂t₃,

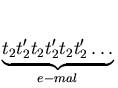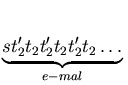t₃t'₂t₂t₃t'₂t₂ = t'₂t₂t₃t'₂t₂t₃, $\underbrace{t_2st'_2t_2t'_2t_2t'_2 \hdots}_{e-mal}^{}\,$ = $\underbrace{st'_2t_2t'_2t_2t'_2t_2 \hdots}_{e-mal}^{}\,$ .

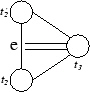Der Graph $\epsfig{file=../Diagramme/Bsp2.eps}$ entspricht der Präsentation

t'₂² = t₂² = t₃² = 1, t'₂t₃t'₂ = t₃t'₂t₃, t₂t₃t₂ = t₃t₂t₃,

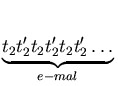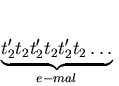t₃t'₂t₂t₃t'₂t₂ = t'₂t₂t₃t'₂t₂t₃, $\underbrace{t_2t'_2t_2t'_2t_2t'_2 \hdots}_{e-mal}^{}\,$ = $\underbrace{t'_2t_2t'_2t_2t'_2t_2 \hdots}_{e-mal}^{}\,$ .

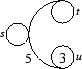Der Graph $\epsfig{file=../Diagramme/G15.eps}$ entspricht der Präsentation

s² = t² = u³ = 1, stu = tus, ustut = stutu.

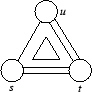Der Graph $\epsfig{file=../Diagramme/G24.eps}$ entspricht der Präsentation

s² = t² = u² = 1, stst = tsts, tutu = utut, utusut = sutusu, sus = usu.

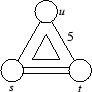Der Graph $\epsfig{file=../Diagramme/G27.eps}$ entspricht der Präsentation

s² = t² = u² = 1, stst = tsts, tutut = ututu, utusut = sutusu, sus = usu.

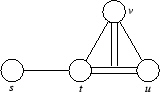Der Graph $\epsfig{file=../Diagramme/G29.eps}$ entspricht der Präsentation

s² = t² = u² = v² = 1, sv = vs, su = us, sts = tst, vtv = tvt, uvu = vuv, tutu = utut, vtuvtu = tuvtuv.

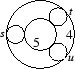Der Graph $\epsfig{file=../Diagramme/G13.eps}$ entspricht der Präsentation

s² = t² = u² = 1, ustus = stust, tust = ustu.

Nun eine Übersicht über die Graphen der Gruppen. Die exceptionellen sind nach Namen geordnet (die Reihenfolge entspricht damit der Reihenfolge bei Shephard und Todd).
Um nähere Eigenschaften der Graphen zu erfahren, einfach die Graphen anklicken.

Tabelle: Graphen der 34 exceptionellen irreduziblen komplexen Spiegelungsgruppen

Name

Graph

Grade

G₄

$\epsfig{file=../Diagramme/G4.eps}$

4, 6

G₅

$\epsfig{file=../Diagramme/G5.eps}$

6, 12

G₆

$\epsfig{file=../Diagramme/G6.eps}$

4, 12

G₇

$\epsfig{file=../Diagramme/G7.eps}$

12, 12

G₈

$\epsfig{file=../Diagramme/G8.eps}$

8, 12

G₉

$\epsfig{file=../Diagramme/G9.eps}$

8, 24

G₁₀

$\epsfig{file=../Diagramme/G10.eps}$

12, 24

G₁₁

$\epsfig{file=../Diagramme/G11.eps}$

24, 24

G₁₂

$\epsfig{file=../Diagramme/G12.eps}$

6, 8

G₁₃

$\epsfig{file=../Diagramme/G13.eps}$

8, 12

G₁₄

$\epsfig{file=../Diagramme/G14.eps}$

6, 24

G₁₅

$\epsfig{file=../Diagramme/G15.eps}$

12, 24

G₁₆

$\epsfig{file=../Diagramme/G16.eps}$

20, 30

G₁₇

$\epsfig{file=../Diagramme/G17.eps}$

20, 60

G₁₈

$\epsfig{file=../Diagramme/G18.eps}$

30, 60

G₁₉

$\epsfig{file=../Diagramme/G19.eps}$

60, 60

G₂₀

$\epsfig{file=../Diagramme/G20.eps}$

12, 30

G₂₁

$\epsfig{file=../Diagramme/G21.eps}$

12, 60

G₂₂

$\epsfig{file=../Diagramme/G22.eps}$

12, 20

G₂₃

$\epsfig{file=../Diagramme/G23.eps}$

2, 6, 10

G₂₄

$\epsfig{file=../Diagramme/G24.eps}$

4, 6, 14

G₂₅

$\epsfig{file=../Diagramme/G25.eps}$

6, 9, 12

G₂₆

$\epsfig{file=../Diagramme/G26.eps}$

6, 12, 18

G₂₇

$\epsfig{file=../Diagramme/G27.eps}$

6, 12, 30

G₂₈

$\epsfig{file=../Diagramme/G28.eps}$

2, 6, 8, 12

G₂₉

$\epsfig{file=../Diagramme/G29.eps}$

4, 8, 12, 20

G₃₀

$\epsfig{file=../Diagramme/G30.eps}$

2, 12, 20, 30

G₃₁

$\epsfig{file=../Diagramme/G31.eps}$

8, 12, 20, 24

G₃₂

$\epsfig{file=../Diagramme/G32.eps}$

12, 18, 24, 30

G₃₃

$\epsfig{file=../Diagramme/G33.eps}$

4, 6, 10, 12, 18

G₃₄

$\epsfig{file=../Diagramme/G34.eps}$

6, 12, 18, 24, 30, 42

G₃₅

$\epsfig{file=../Diagramme/G35.eps}$

2, 5, 6, 8, 9, 12

G₃₆

$\epsfig{file=../Diagramme/G36.eps}$

2, 6, 8, 10, 12, 14, 18

G₃₇

$\epsfig{file=../Diagramme/G37.eps}$

2, 8, 12, 14, 18, 20, 24, 30

Bemerkung 1.7
Unter diesen 34 komplexen Spiegelungsgruppen sind einige, die reell realisiert werden können. Man kann das am Graphen daran erkennen, daß alle Erzeuger Involutionen sind und nur Verbindungen zwischen jeweils zwei Knoten auftauchen, also keine Kreise oder Dreiecke, weil es bei der Präsentation als Coxetergruppe nur Relationen zwischen jeweils zwei Erzeugern gibt. G₂₃, G₂₈, G₃₀, G₃₅, G₃₆ und G₃₇ sind reelle Spiegelungsgruppen.

**Tabelle:** Graphen der sechs Serien
Name	Graph	Grade

G(de, e, r), 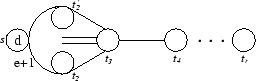e > 2, d $\geq$ 2	$\epsfig{file=../Diagramme/Gdeer.eps}$	ed, 2ed,(r - 1)ed, rd

S_{r + 1}	$\epsfig{file=../Diagramme/Sr.eps}$	2, 3, r + 1

G(d, 1, r), d $\geq$ 2	$\epsfig{file=../Diagramme/Gd1r.eps}$	d, 2d, rd

G(2d, 2, r), d 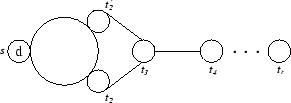$\geq$ 2	$\epsfig{file=../Diagramme/G2d2r.eps}$	2d, 4d, 2(r - 1)d, rd

G(e, e, r), e 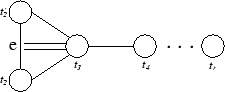$\geq$ 2, r > 2	$\epsfig{file=../Diagramme/Geer.eps}$	e, 2e,(r - 1)e, r

G(e, e, 2), e $\geq$ 3	$\epsfig{file=../Diagramme/Gee2.eps}$	2, e

Bemerkung 1.8
Zwei der Serien sind reell realisierbar, die zweite, die symmetrischen Gruppen S_{r + 1}, und die sechste, G(e, e, 2), e $\geq$ 2.

Jahn, Heinz, Todorovic 2002-02-28