Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Gruppentheorie - Einleitung - Beispiele

Symmetrische Gruppe

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Für eine beliebige Menge $ M$ bilden die Bijektionen von $ M$ in $ M$, versehen mit der Komposition von Abbildungen als Operation, eine Gruppe, die sogenannte symmetrische Gruppe von $ M$.

Ist $ M = \{1, 2, \dots, n\}$, so spricht man von der symmetrischen Gruppe $ S_n$ vom Grad $ n$. Die $ n!$ Elemente $ \pi$ von $ S_n$ nennt man Permutationen und benutzt die Schreibweise

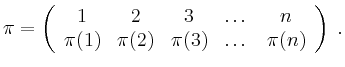
$\displaystyle \pi=\left( \begin{array}{ccccc} 1 & 2 & 3 & \dots & n \\ \pi(1) & \pi(2) & \pi(3) & \dots & \pi(n) \end{array} \right) \; . $

Dabei stehen in der oberen Zeile die Elemente der Menge in der natürlichen Reihenfolge, darunter dann jeweils ihre Bilder unter $ \pi$.

Die Permutationsgruppe ist im Allgemeinen nicht kommutativ.

Permutationen werden auch in der so genannten Zyklenschreibweise angegeben. Dabei besteht ein Zyklus aus einem Element und seinen Bildern bei mehrfacher Ausführung der Permutation, bis wieder das ursprüngliche Element erreicht wird. Aus den Elementen, die im ersten Zyklus nicht vorkommen, werden weitere Zyklen gebildet, bis alle Elemente auftreten. Die Zyklen werden nach der Anzahl der Elemente absteigend sortiert und jeweils in runden Klammern hintereinander geschrieben. Zyklen der Länge 1 werden meist weggelassen.

Beispielsweise ist

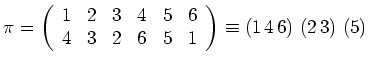$\displaystyle \pi = \left( \begin{array}{cccccc} 1 & 2 & 3 & 4 & 5 & 6 \\ 4 & 3 & 2 & 6 & 5 & 1 \end{array}\right) \equiv (1 \, 4 \, 6) \ (2 \, 3) \ (5)$    bzw. $\displaystyle \pi = (1 \, 4 \, 6) \ (2 \, 3) \; . $

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 14.11.2008