Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Gruppentheorie - Kristallographische Gruppen - Kristallographische Punktgruppen

Endliche Untergruppen der SO(3)

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]

Sei $ G\neq 1$ endliche Untergruppe von $ SO(3,\mathbb{R})$ . Dann gilt:

a)
Es existieren nur endlich viele Pole von $ G$ .
b)
Seien $ v_1,\dots,v_k$ ein Repräsentantensystem der Konjugiertenklassen von Polen von $ G$ und $ m_i=\vert G_{v_i} \vert$ . Dann gilt

$\displaystyle m_i\geq2, \quad m_i \textnormal{ teilt } \vert G\vert$

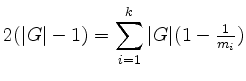
$\displaystyle 2(\vert G\vert-1) = \sum_{i=1}^k \vert G\vert(1-\tfrac{1}{m_i})$

c)
Die möglichen Lösungen der Gleichungen aus b) sind:
  1. $ k=2$ : $ m_1=m_2=\vert G\vert$ mit $ \vert G\vert$ beliebig
  2. $ k=3$ : $ m_1=m_2=2$ , $ m_3=\tfrac{\vert G\vert}{2}$ mit $ \vert G\vert\geq4$ gerade
  3. $ k=3$ : $ m_1=2$ , $ m_2=3$ , $ m_3=3$ , $ \vert G\vert=12$
  4. $ k=3$ : $ m_1=2$ , $ m_2=3$ , $ m_3=4$ , $ \vert G\vert=24$
  5. $ k=3$ : $ m_1=2$ , $ m_2=3$ , $ m_3=5$ , $ \vert G\vert=60$
Alle Fälle tauchen auf und führen zu den folgenden Gruppen:

  1. führt auf Zyklische Gruppen $ C_n$ , erzeugt durch Drehung um den Winkel $ \frac{2\pi}{n}$ um eine feste Achse.

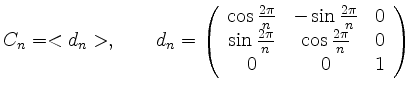
    $\displaystyle C_n = <d_n> , \qquad d_n = \left( \begin{array}{ccc} \cos{ \frac{... ...\frac{2 \pi}{n}} & \cos{ \frac{2 \pi}{n}} & 0\\ 0 & 0 & 1 \end{array} \right) $

  2. führt auf Diedergruppen $ D_n$ , erzeugt durch Drehung um den Winkel $ \frac{2\pi}{n}$ und einer Spiegelung.

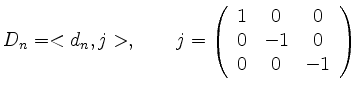
    $\displaystyle D_n = <d_n,j> , \qquad j= \left( \begin{array}{ccc} 1 & 0 & 0\\ 0 & -1 & 0\\ 0 & 0 & -1\\ \end{array} \right) $

  3. führt auf die Drehgruppe des Tetraeders $ T \cong A_4$ .

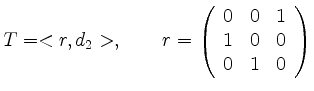
    $\displaystyle T = <r,d_2> , \qquad r= \left( \begin{array}{ccc} 0 & 0 & 1\\ 1 & 0 & 0\\ 0 & 1 & 0 \end{array} \right) $

  4. führt auf die Drehgruppe des Oktaeders $ O \cong S_4$ .

    $\displaystyle O = <r,d_4> $

  5. führt auf die Drehgruppe des Ikosaeders $ I \cong A_5$ .

    $\displaystyle I = <r,t> , \qquad t= \frac{1}{2} \left( \begin{array}{ccc} 1 & -... ... \sqrt{5} \right) & 1 & \frac{1}{2}\left(1+\sqrt{5}\right) \end{array} \right) $

Dies liefert also eine vollständige Liste der Konjugationsklassen endlicher Untergruppen von $ SO(3,\mathbb{R})$ :
$ C_n,D_k,T,O,I$ mit $ n,k\in \mathbb{N}$ und $ k\geq 2$ .

(Autor: Baur)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 14.11.2008