Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Gruppentheorie - Klassische Matrixgruppen - Orhtogonale und unitäre Gruppen

Die Gruppe SU(2)

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Sei $ h$ eine symmetrische Bilinearform auf $ \mathbb{R}^{4}$ definiert durch:

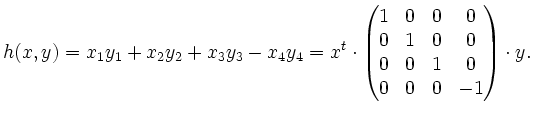
$\displaystyle h(x,y) = x_{1}y_{1} + x_{2}y_{2} + x_{3}y_{3} - x_{4}y_{4} = x^{t... ...begin{pmatrix} 1&0&0&0 \\ 0&1&0&0 \\ 0&0&1&0 \\ 0&0&0&-1 \end{pmatrix} \cdot y.$

Dann heisst das Paar $ (\mathbb{R}^{4}, h)$ Minkowski-Raum.

Physikalische Interpretation:
Wählt man $ \cal B$ = $ \{ e_{1}, e_{2}, e_{3}, \frac{e_{4}}{c}\}$ als Basis von $ \mathbb{R}^{4}$, wobei $ c$ die Lichtgeschwindigkeit ist, so hat $ h$ bzgl. dieser Basis folgende Darstellung:

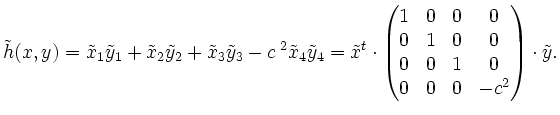
$\displaystyle \tilde{h}(x,y) = \tilde{x}_{1}\tilde{y}_{1} + \tilde{x}_{2}\tilde... ...ix}1&0&0&0 \\ 0&1&0&0 \\ 0&0&1&0 \\ 0&0&0&-c^{2} \end{pmatrix} \cdot \tilde{y}.$

Es werden folgende Bezeichnungen eingeführt: Sind $ (x_{1}, x_{2}, x_{3})$ die räumlichen Koordinaten eines Punktes, $ x_{4} = t$ die Zeit, so werden die 4-Tupel $ (x_{1}, x_{2}, x_{3}, t)$ Weltpunkte genannt. Ein vom Raumpunkt $ (0,0,0)$ ausgehendes Lichtsignal erreicht im Vakuum zur Zeit $ t$ gerade die Raumpunkte $ (x_{1}, x_{2}, x_{3}, t)$ mit

$\displaystyle x_{1}^{2} + x_{2}^{2} + x_{3}^{2} = c^{2}t^{2},$

d.h. Lichtvektoren sind genau die Weltpunkte, welche das Lichtsignal irgendwann erreicht.

Die zeitartigen Vektoren sind die Weltpunkte, welche von $ (0,0,0)$ aus mit einem Signal erreicht werden können, dessen Ausbreitungsgeschwindigkeit kleiner ist, als die Lichtgeschwindigkeit.

Nimmt man die Hypothese an, dass sich keine Wirkung schneller als mit Lichtgeschwindigkeit ausbreiten kann (eine der Behauptungen der speziellen Relativitätstheorie), so stehen die Raumvektoren in keinerlei Kausalzusammenhang mit dem Weltpunkt $ (0,0,0,0)$.

(Autor: Borgart)
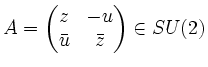Sei $ A = \begin{pmatrix}z & -u\\ \bar{u} & \bar{z} \end{pmatrix} \in SU(2)$. Die Zahlen 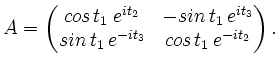$ z$ und $ u$ haben eine Darstellung in Polarkoordinaten,
d.h. es gibt $ r, s \in \mathbb{R}_{+}$ und $ t_{2}, t_{3} \in [0,2\pi]$ so, dass

$\displaystyle z = re^{it_{2}} \hspace{0.3cm} und \hspace{0.3cm} u = se^{it_{3}}.$

Wegen det$ A$ = 1 gilt $ r^2 +s^2$ = 1, d.h. es gibt ein $ t_{1} \in [0,\pi]$ so, dass

$\displaystyle r = cos \, t_{1} \hspace{0.3cm} und \hspace{0.3cm} s = sin \,t_{1}.$

Also hat $ A$ folgende Form

$\displaystyle A= \begin{pmatrix}cos \,t_{1}\,e^{it_{2}} & -sin\, t_{1}\,e^{it_{3}}\\ sin \, t_{1} \, e^{-it_{3}} & cos \, t_{1} \, e^{-it_{2}} \end{pmatrix}.$

Setzt man $ \alpha = t_{1},\hspace{0.2cm} \beta = \frac{t_{2}+t_{3}}{2},\hspace{0.2cm} \gamma = \frac{t_{2}-t_{3}}{2},$ so erhält man

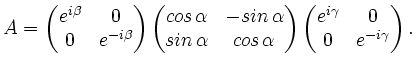
$\displaystyle A = \begin{pmatrix}e^{i\beta} & 0\\ 0 & e^{-i\beta} \end{pmatrix}... ...a \end{pmatrix}\begin{pmatrix}e^{i\gamma} & 0\\ 0 & e^{-i\gamma} \end{pmatrix}.$

(Autor: Borgart)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 14.11.2008