[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
	Mathematik-Online-Kurs: Gruppentheorie - Einleitung - Grundlegende Definitionen und Notationen
	Gruppenordnung, Elementordnung

Eine Gruppe 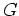heißt endlich, wenn sie nur endlich viele Elemente besitzt. Die Anzahl der Elemente einer endlichen Gruppe 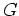heißt Ordnung 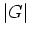von .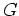

Ist 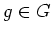und gibt es ein 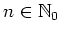mit 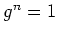, dann nennt man das kleinste solche 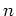die Ordnung des Elements 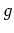. 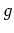heißt dann Element endlicher Ordnung oder auch Torsionselement.

Bemerkung: In endlichen Gruppen hat jedes Element endliche Ordnung. Umgekehrt gibt es aber durchaus unendliche Gruppen in denen jedes Element endliche Ordnung hat.