Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: LaTeX - Darstellung mathematischer Ausdrücke

Fortsetzungspunkte

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Zur Darstellung von Fortsetzungspunkten stehen im mathematischen Modus die folgenden Befehle zur Verfügung
$\ldots$\ \ \verb\vert\ldots\vert \qquad $\cdots$\ \ \verb\vert\cdots\vert \qqu... ...$\vdots$\ \ \verb\vert\vdots\vert \qquad $\ddots$\ \ \verb\vert\ddots\vert \,.
Eine besondere Funktionalität besitzt der Befehl \dots, der sowohl im Absatzmodus, als auch im mathematischen Modus zur Darstellung von Fortsetzungspunkten verwendet werden kann. Im mathematischen Modus wird zudem die Position der Punkte automatisch gesteuert. Sie erscheinen zentriert, sofern sie zwischen Operatoren bzw. Relationen auftreten. Andernfalls erscheinen sie auf der Grundlinie.

So ergibt zum Beispiel 

  \[
    \sum_{k=0}^{n} a_{k}x^{k}=a_{0}+a_{1}x+\dots+a_{n}x^{n}
    \qquad \text{und} \qquad
    \sum_{k=0}^{\infty} a_{k}x^{k}=a_{0}+a_{1}x+\dots 
  \]
die Ausgabe

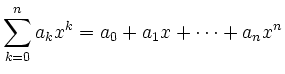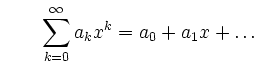
$\displaystyle \sum_{k=0}^{n} a_{k}x^{k}=a_{0}+a_{1}x+\dots+a_{n}x^{n}$   und$\displaystyle \qquad \sum_{k=0}^{\infty} a_{k}x^{k}=a_{0}+a_{1}x+\dots $

(Autor: Joachim Wipper)
Der Quelltext 
  Automatische Positionierung der Punkte bei \verb|\dots|:
  \[
    (a_n)=a_0,a_1,\dots \quad \text{und}\quad
    \sum_{k_1=1}^m \dots \sum_{k_n=1}^m 1= m^n
  \] 
  Determinante der Vandermond-Matrix (manuelle Positionierung):
  \[
    \left|\left(
    \begin{array}{ccccc}
      1 & x_1 & x_1^2 & \cdots & x_1^{n-1} \\
      1 & x_2 & x_2^2 & \cdots & x_2^{n-1} \\
      \vdots & \vdots & \vdots & \ddots & \vdots \\     
      1 & x_n & x_n^2 & \cdots & x_n^{n-1} \\
    \end{array}
    \right)\right|=\prod_{k>j}(x_k-x_j)
  \]
  Für die Darstellung von Mehrfachintegralen mit Fortsetzungspunkten
  stellt das {\tt amsmath}-Paket den Befehl \verb|\idotsint| zur
  Verfügung:
  \medskip

  Volumen des Bereichs $A\subset \mathbb{R}^{n}$:
  \[
    \operatorname{vol}(A)=\idotsint\limits_{A}1\,dx_{1} \dots dx_{n}
  \]
ergibt
\includegraphics[width=14cm]{bsp_fortsetzungspunkte.eps}

(Autor: Joachim Wipper)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 24.2.2009