Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Mathematik II für Informatik und Softwaretechnik - Lösungen - Übungsblatt 5

Blatt 5, Aufgabe 5

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]

Berechnen Sie die Werte der gegebenen Integrale:

a)

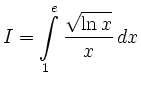
$\displaystyle I = \int\limits^e_1\frac{\sqrt{\ln x}}{x}\,dx $


Ansatz mit Substitution:

$\displaystyle u = \ln x $

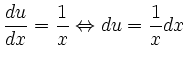
$\displaystyle \frac{du}{dx} = \frac{1}{x} \Leftrightarrow du = \frac{1}{x}dx $

$\displaystyle \longrightarrow I = \int\limits^{x=e}_{x=1}\sqrt{u}\,du = \left[\frac{2}{3}u\sqrt{u}\right]^{x=e}_{x=1} $

Resubstitution ergibt:

$\displaystyle u = \ln x $


$\displaystyle \longrightarrow I$ $\displaystyle =$ $\displaystyle \left[\frac{2}{3}\ln x\sqrt{\ln x}\right]^e_1$  
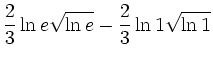  $\displaystyle =$ $\displaystyle \frac{2}{3}\ln e\sqrt{\ln e} - \frac{2}{3}\ln 1\sqrt{\ln 1}$  
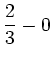  $\displaystyle =$ $\displaystyle \frac{2}{3} - 0$  
  $\displaystyle =$ $\displaystyle \frac{2}{3}$  

b)

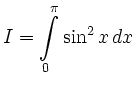
$\displaystyle I = \int\limits^\pi_0\sin^2x\,dx $


Ansatz mit partieller Integration:

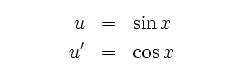
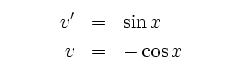
$\textstyle \parbox{5.0cm}{ \begin{eqnarray*} u & = &\sin x \\ u' & = &\cos x \end{eqnarray*}}$ $\textstyle \parbox{5.0cm}{ \begin{eqnarray*} v' & = &\sin x \\ v & = &-\cos x \end{eqnarray*}}$

$\displaystyle \longrightarrow I = \left[-\sin x\cos x\right]^\pi_0 + \int\limits^\pi_0\cos^2x\,dx $

$\displaystyle \cos^2x + \sin^2x = 1 \Leftrightarrow \cos^2x = 1 - \sin^2x $


$\displaystyle \longrightarrow I$ $\displaystyle =$ $\displaystyle \left[-\sin x\cos x\right]^\pi_0 + \int\limits^\pi_0(1 - \sin^2x)\,dx$  
  $\displaystyle =$ $\displaystyle \left[-\sin x\cos x\right]^\pi_0 + \int\limits^\pi_0 1\,dx - \int\limits^\pi_0 \sin^2x\,dx$  
  $\displaystyle =$ $\displaystyle \left[-\sin x\cos x + x\right]^\pi_0 - I$  


$\displaystyle \Leftrightarrow 2I$ $\displaystyle =$ $\displaystyle \left[x - \sin x\cos x\right]^\pi_0$  
$\displaystyle \Leftrightarrow I$ $\displaystyle =$ $\displaystyle \left[\frac{x - \sin x\cos x}{2}\right]^\pi_0$  
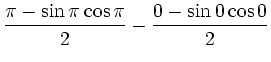  $\displaystyle =$ $\displaystyle \frac{\pi - \sin\pi\cos\pi}{2} - \frac{0 - \sin0\cos0}{2}$  
  $\displaystyle =$ $\displaystyle \frac{\pi}{2}$  

c)

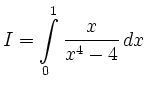
$\displaystyle I = \int\limits^1_0\frac{x}{x^4 - 4}\,dx $


Ansatz mit Partialbruchzerlegung:

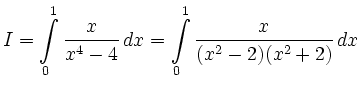
$\displaystyle I = \int\limits^1_0\frac{x}{x^4 - 4}\,dx = \int\limits^1_0\frac{x}{(x^2 - 2)(x^2 + 2)}\,dx $


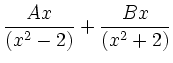$\displaystyle \frac{x}{(x^2 - 2)(x^2 + 2)}$ $\displaystyle =$ $\displaystyle \frac{Ax}{(x^2 - 2)} + \frac{Bx}{(x^2 + 2)}$  
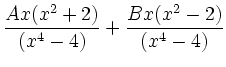  $\displaystyle =$ $\displaystyle \frac{Ax(x^2 + 2)}{(x^4 - 4)} + \frac{Bx(x^2 - 2)}{(x^4 - 4)}$  
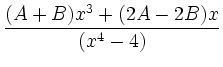  $\displaystyle =$ $\displaystyle \frac{(A + B)x^3 + (2A - 2B)x}{(x^4 - 4)}$  

Koeffizientenvergleich ergibt:

$\displaystyle A + B$ $\displaystyle =$ 0  
$\displaystyle 2A - 2B$ $\displaystyle =$ $\displaystyle 1$  

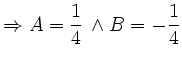
$\displaystyle \Rightarrow A = \frac{1}{4}\, \land B = -\frac{1}{4} $

Einsetzen von A und B ergibt:

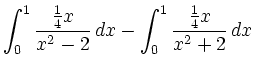$\displaystyle \longrightarrow I$ $\displaystyle =$ $\displaystyle \int^1_0\frac{\frac{1}{4}x}{x^2 - 2}\,dx - \int^1_0\frac{\frac{1}{4}x}{x^2 + 2}\,dx$  
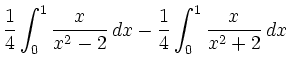  $\displaystyle =$ $\displaystyle \frac{1}{4}\int^1_0\frac{x}{x^2 - 2}\,dx - \frac{1}{4}\int^1_0\frac{x}{x^2 + 2}\,dx$  
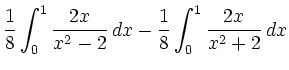  $\displaystyle =$ $\displaystyle \frac{1}{8}\int^1_0\frac{2x}{x^2 - 2}\,dx - \frac{1}{8}\int^1_0\frac{2x}{x^2 + 2}\,dx$  
  $\displaystyle =$ $\displaystyle \left[\frac{1}{8}\ln \vert x^2 - 2\vert - \frac{1}{8}\ln \vert x^2 + 2\vert\right]^1_0$  
  $\displaystyle =$ $\displaystyle \frac{1}{8}\left[\ln \vert-1\vert - \ln \vert 3\vert - \ln \vert-2\vert + \ln \vert 2\vert\right]$  
  $\displaystyle =$ $\displaystyle \frac{1}{8}\left[\ln 1 - \ln 3 - \ln 2 + \ln 2\right]$  
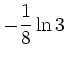  $\displaystyle =$ $\displaystyle -\frac{1}{8}\ln 3$  

(Prof. Dr. Eberhard Teufel, Dr. Norbert Röhrl)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 28.10.2006