Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Integralrechnung - Integrationsregeln

Variablensubstitution

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Aus der Kettenregel

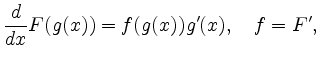
$\displaystyle \frac{d}{dx} F(g(x))=f(g(x)) g'(x),\quad f=F',$

folgt durch Bilden von Stammfunktionen für eine Substiution $ y=g(x)$

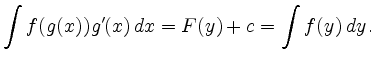
$\displaystyle \int f(g(x)) g'(x)\, dx = F(y) +c=\int f(y)\,dy \,.$

Entsprechend gilt

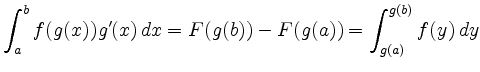
$\displaystyle \int_a^b f(g(x)) g'(x) \, dx = F(g(b))-F(g(a)) = \int_{g(a)}^{g(b)}f(y)\, dy $

für bestimmte Integrale. Mit Hilfe von Differentialen läßt sich diese Formel in der Form

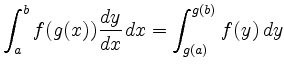
$\displaystyle \int_a^b f(g(x)) \frac{dy}{dx}\,dx = \int_{g(a)}^{g(b)} f(y)\,dy $

schreiben.

Ein einfacher Spezialfall ist eine lineare Variablensubstitution:

$\displaystyle x \mapsto y = px +q\,. $

In diesem Fall ist

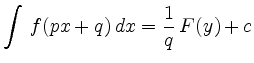
$\displaystyle \int\,f(px+q)\,dx = \frac{1}{q}\,F(y) + c $

bzw.

$\displaystyle \int_{a}^{b}\,f(px+q)\,dx = \frac{1}{p}\,[F]_{pa+q}^{pb+q}\,. $

(Inhalt vorübergehend nicht verfügbar)

(Inhalt vorübergehend nicht verfügbar)

(Inhalt vorübergehend nicht verfügbar)
Ist die innere Ableitung im Integranden erkennbar, wie beispielsweise für

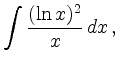
$\displaystyle \int \frac{(\ln x)^2}{x} \, dx\,, $

so ist die Anwendung der Substitutionsregel besonders einfach. In dem Beispiel setzt man

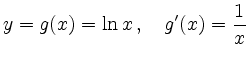
$\displaystyle y = g(x)= \ln x \,, \quad g^\prime (x) =\frac{1}{x} $

und erhält

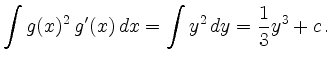
$\displaystyle \int g(x)^2\, g^\prime (x) \, dx = \int y^2 \,dy=\frac{1}{3}y^3+c\, . $

Nach Rücksubstitution ergibt sich

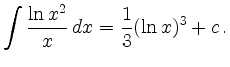
$\displaystyle \int \frac{\ln x ^2}{x} \, dx = \frac{1}{3}(\ln x)^3+c\,. $

(Autoren: Höllig/Kopf)
Typischerweise versucht man durch Substitution den Integranden zu vereinfachen. Beispielsweise liegt es für

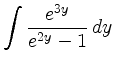
$\displaystyle \int \frac{e^{3y}}{e^{2y}-1}\, dy $

nahe

$\displaystyle y=g(x)=\ln x \quad \Leftrightarrow \quad x=e^y $

zu setzen. Dies ergibt wegen

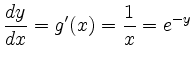
$\displaystyle \frac{dy}{dx}=g^\prime (x)= \frac{1}{x}=e^{-y} $

das transformierte unbestimmte Integral
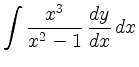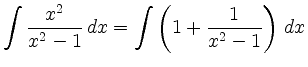$\displaystyle \int \frac{x^3}{x^2-1} \, \frac{dy}{dx} \, dx$ $\displaystyle =$ $\displaystyle \int \frac{x^2}{x^2-1}\,dx = \int \left( 1+\frac{1}{x^2-1} \right)\, dx$  
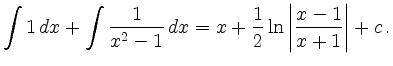  $\displaystyle =$ $\displaystyle \int 1\,dx + \int \frac{1}{x^2-1}\,dx = x + \frac{1}{2} \ln \left\vert \frac{x-1}{x+1} \right\vert +c \,.$  

Durch Rücksubstitution von $ x=e^y$ erhält man schließlich

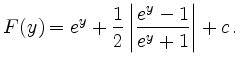
$\displaystyle F(y)=e^y+\frac{1}{2} \left\vert \frac{e^y-1}{e^y+1} \right\vert+c\,. $

(Autoren: Höllig/Kopf)
Die Stammfunktion

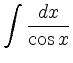
$\displaystyle \int \frac{dx}{\cos x} $

läßt sich mit der Substitution

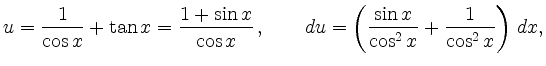
$\displaystyle u=\frac{1}{\cos x}+ \tan x=\frac{1+\sin x}{\cos x}\,, \qquad du=\left(\frac{\sin x}{\cos^2 x}+\frac{1}{\cos^2 x}\right)\,dx, $

berechnen:
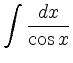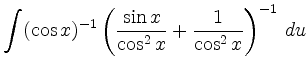$\displaystyle \int \frac{dx}{\cos x} $ $\displaystyle =$ $\displaystyle \int (\cos x)^{-1}\left(\frac{\sin x}{\cos^2 x}+\frac{1}{\cos^2 x}\right)^{-1}\,du$  
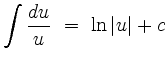  $\displaystyle =$ $\displaystyle \int \frac{du}{u} \ = \ \ln \vert u\vert+c$  
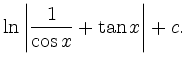  $\displaystyle =$ $\displaystyle \ln \left\vert \frac{1}{\cos x} + \tan x \right\vert +c.$  

Eine Anwendung ist die Mercator-Projektion. Hierbei wird die Erdoberfläche winkeltreu auf eine Ebene projiziert.

\includegraphics[height=3cm]{bsp_mercator_bild1.eps}      \includegraphics[height=3cm]{bsp_mercator_bild2.eps}

Die Breitenkreise werden dabei mit dem Verhältnis $ 1/\cos \theta$ gestreckt.

(Autoren: Höllig/Kopf)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.1.2017