Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Vorkurs Mathematik - Aufgaben - Grundlagen

Abbildungen

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Drücken Sie die folgenden Aussagen über eine Abbildung 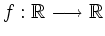$ f: \mathbb{R}\longrightarrow\mathbb{R}$ in formaler Schreibweise aus:

a) 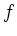$ f$ ist nicht surjektiv  b) 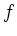$ f$ ist nicht injektiv
c) 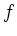$ f$ ist nicht bijektiv  d) 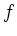$ f$ ist weder surjektiv noch injektiv
(Autor: Christian Apprich)
Untersuchen Sie, ob die folgenden Abbildungen $ f: \mathbb{R} \rightarrow \mathbb{R}$ surjektiv, injektiv oder bijektiv sind:

$\displaystyle {\bf a)} \quad f(x)=x\sin x \qquad {\bf b)} \quad f(x)=\exp\left(-x^{3}+1\right) \qquad {\bf c)} \quad f(x)=x\ln \frac{1}{\vert x\vert+1} $

Antwort:


a)     
$ f$ ist surjektiv.          keine Angabe         wahr         falsch
$ f$ ist injektiv.          keine Angabe         wahr         falsch
$ f$ ist bijektiv.          keine Angabe         wahr         falsch


b)     
$ f$ ist surjektiv.          keine Angabe         wahr         falsch
$ f$ ist injektiv.          keine Angabe         wahr         falsch
$ f$ ist bijektiv.          keine Angabe         wahr         falsch


c)     
$ f$ ist surjektiv.          keine Angabe         wahr         falsch
$ f$ ist injektiv.          keine Angabe         wahr         falsch
$ f$ ist bijektiv.          keine Angabe         wahr         falsch


  

[Andere Variante]
(Autor: Joachim Wipper)
Wie viele Relationen gibt es zwischen zwei jeweils dreielementigen Mengen $ A$ und $ B$ ? Wie viele davon sind Abbildungen und wie viele der Abbildungen sind surjektiv?

Lösung:

Relationen gesamt:
Abbildungen:
surjektive Abbildungen:

   

(Autoren: Hörner/Lesky)
Bestimmen Sie für die Mengen

$\displaystyle A=\{a_1,a_2,a_3\}$   und$\displaystyle \qquad B=\{b_1,b_2,b_3,b_4\}\,.$

die Anzahl $ n_R$ der unterschiedlichen Relationen zwischen $ A$ und $ B$ sowie die Anzahl $ n_A$ der verschiedenen Abbildungen von $ A$ in $ B$. Wie viele dieser Abbildungen sind injektiv, surjektiv, bijektiv?

Antwort:
$ n_R=$ $ n_A=$      
injektiv:     surjektiv:     bijektiv:  


  

[Andere Variante]
(Aus: 1. Scheinklausur HM I, K. Höllig, WS 2004/2005)
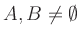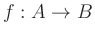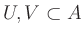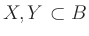Gegeben sind die Mengen $ A,B\neq \emptyset$, eine Abbildung $ f:A\rightarrow B$ sowie die Teilmengen $ U,V\subset A$ und $ X,Y\subset B$. Zeigen bzw. widerlegen Sie mit Hilfe eines geeigneten Gegenbeispiels die folgenden Beziehungen:
a)     $ f(U\cup V)=f(U)\cup f(V)$          b)     $ f(U\cap V)=f(U)\cap f(V)$
c)     $ f^{-1}(X\cup Y)=f^{-1}(X)\cup f^{-1}(Y)$          d)     $ f^{-1}(X\cap Y)=f^{-1}(X)\cap f^{-1}(Y)$
(Autor: Joachim Wipper)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 9.6.2009