Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Vorkurs Mathematik - Aufgaben - Analysis

Funktionen

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Bestimmen Sie alle Nullstellen der Polynome

   a)$\displaystyle \quad x^3+3x^2-9x+5$   b)$\displaystyle \quad x^3-3x^2+4x-12 $

Antwort:
a)
,     ,         
b)
$ \mathrm{i}$,      $ \mathrm{i}$,         
(aufsteigend sortiert)
   
(Autor: Marco Boßle)
Schon kurz nach Studienbeginn ist Freshman Felix überzeugt, zur Lösung der HM-Aufgaben einen High-End PC zu benötigen.

Kosten: 5000 DM - Sparbuchstand: 0 DM.

a)
Seine Bank bietet ihm einen Kredit, der durch $ 24$ gleich große Monatsraten getilgt werden soll. Die Restschuld wird monatlich mit $ 1\%$ verzinst; die erste Rate wird einen Monat nach Kreditaufnahme bezahlt. Wie hoch sind die Monatsraten $ r$ anzusetzen?

b)
Felix entschließt sich, den Kredit ohne Ratenzahlungen nach zwei Jahren zurückzubezahlen. Wie hoch ist diese Summe bei jährlicher, vierteljährlicher, monatlicher, täglicher oder stetiger Verzinsung mit $ 12\%$ bzw. $ 3\%$ bzw. $ 1\%$ ...? Bestimmen Sie jeweils den jährlichen Effektivzins.

Aufgrund seines sehr guten Diploms beginnt Felix Sparmann bei der Raffzahn GmbH mit einem Anfangsgehalt von 4000 EUR. Man eröffnet ihm jedoch, dass nur jährliche Gehaltserhöhungen von 3 % zu erwarten sind. Sparmann vertraut dieser Prognose, da die Firma Raffzahn auf ihn insbesondere wegen des betriebsinternen Pensionsfonds RaffRent (5 % effektiver Jahreszins, monatliche Zinsgutschrift, garantierte Rückzahlung der Einlagen) einen soliden Eindruck macht. Er beschließt, 20 % seines stetig steigenden Gehalts 40 Jahre (=65-25) lang jeweils am Monatsersten einzuzahlen.

Berechnen Sie, welche monatliche Rente (unmittelbar nach Ansparzeitraum, Auszahlung jeweils am Monatsersten) er über einen Zeitraum von 20 Jahren (=85-65) aus dem angesparten Kapital schöpfen kann, und beurteilen Sie, ob Sparmanns Traum von einem Altersruhesitz in Monte Carlo realistisch ist.

Hinweis: Führen Sie eine mathematische Berechnung ohne Berücksichtigung der Effekte durch, die durch Rundung der Renten- und Zinsbeträge auf ganze Cent entstehen.

Antwort:

Monatliche Rente auf ganze Cent gerundet: EUR


   

(Autor: Klaus Höllig)
Bestimmen Sie die am jeweiligen Monatsende zu zahlende Rate bei einem Darlehen von $ 100\,000$EUR und einer Laufzeit von $ 10$ Jahren für folgende Konditionen.
a)
$ 100\%$ Auszahlung bei $ \frac{6}{12}\%$ monatlichem Zins
b)
$ 95\%$ Auszahlung bei $ \frac{5}{12}\%$ monatlichem Zins
c)
$ 100\%$ Auszahlung bei $ 6.5\%$ effektivem Jahreszins
Wie muss der Prozentsatz des schlechtesten Angebots angepasst werden, damit es äquivalent zum besten Angebot ist?

Führen Sie eine mathematische Berechnung ohne Berücksichtigung der Effekte durch, die durch Rundung der Raten und Zinsbeträge auf ganze Cent entstehen.


Antwort:
Monatliche Raten:
a) EUR          b) EUR          c) EUR
Der Jahreszinssatz des schlechtesten Angebots muss auf $ \%$ angehoben werden, damit es äquivalent zum besten ist.
(auf zwei Dezimalstellen gerundet)
   

(Autor: Klaus Höllig)
Nach erfolgreichem Studium hat Susanne Sorgfalt eine Arbeitsstelle gefunden, die genau ihren Vorstellungen entspricht. Sie schließt einen Arbeitsvertrag ab, der ihr die Stelle auf 40 Jahre garantiert und nimmt dafür in Kauf, dass Sie nur einmal nach 20 Jahren eine Gehaltserhöhung um 20% erhält.

Sie möchte nun einen Sparvertrag für ihre Rente abschließen. Ihre Bank sichert ihr für die Gesamtlaufzeit einen Jahreszins von 4% zu, wobei die Zinsen jedes Quartal gutgeschrieben werden (effektiver Jahreszins 4.060401%). Welchen Anteil ihres Gehalts in Prozent muss sie während der 40 Jahre jeweils am Monatsende einzahlen, so dass sie danach noch weitere 20 Jahre jeweils am Monatsanfang ihr Endgehalt als Rente erhalten kann.

Gehen Sie davon aus, dass Frau Sorgfalt Ihre Arbeitsstelle zum 1. Juli antritt, d.h. die erste Einzahlung am 31. Juli stattfindet und die Rentenzahlung wiederum am 1. Juli beginnt. Außerdem soll pro Monat ein Zwölftel des Jahreszinses gewährt werden. Führen Sie die Berechnung ohne die Effekte aus, die durch Rundung der Zahlungs- und Zinsbeträge entstehen.

Antwort:

Anteil des Gehalts: $ \%$
(auf eine Dezimalstelle gerundet)


   

(Autor: Jörg Hörner)
Vereinfachen Sie folgende Terme für $ x>y>0$.
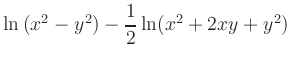
a)     $ \dfrac{\sqrt[3]{x^5\cdot\sqrt[3]{x^2}}}{\sqrt[3]{x^2\cdot\sqrt[6]{x^4}}} \colon \dfrac{\sqrt{x^3\cdot\sqrt[9]{x^7}}}{\sqrt[9]{x^7\cdot\sqrt{x}}}$                          b)     $ \ln\left(x^2-y^2\right)-\dfrac{1}{2}\ln(x^2+2xy+y^2)$

(Autoren: Boßle/Lesky)
Unter der Generationszeit von Bakterien versteht man das für die Verdopplung der Zellzahl erforderliche Zeitintervall $ T$ , das unter anderem von der Beschaffenheit des Kulturmediums abhängt.

Betrachtet werden Bakterien, die auf einem nährstoffreichen Kulturmedium die Generationszeit $ T_1=20$ Minuten und auf einem nährstoffarmen Kulturmedium die Generationszeit $ T_2=50$ Minuten besitzen. Die Anfanspopulation auf dem nährstoffarmen Kulurmedium sei zehnmal größer als die Anfangspopulation auf dem nährstoffreichen Medium. Nach wie viel Minuten sind die beiden Populationen gleich groß?


Antwort:


Minuten

   

(Autor: Joachim Wipper)
Eine Probe enthält zwei gleiche Anteile radioaktiver Materialien mit Halbwertszeiten von $ 10$ und $ 20$ Jahren. Nach wievielen Jahren ist
a)
der Anteil eines der radioaktiven Stoffe an der Gesamtmenge des strahlenden Materials kleiner als ein Prozent?
b)
die Gesamtmenge des strahlenden Materials um die Hälfte reduziert?

Antwort:
a)         b)
(auf vier Dezimalstellen gerundet)


   

(Autor: Klaus Höllig)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 9.6.2009