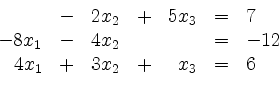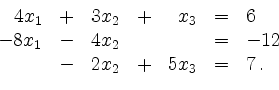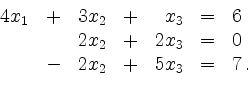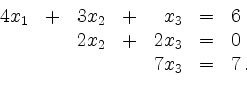Mathematik-Online-Kurs: Vorkurs Mathematik-Lineare Algebra und Geometrie-Lineare Gleichungssysteme-Gauß-Transformation

	[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
	Mathematik-Online-Kurs: Vorkurs Mathematik - Lineare Algebra und Geometrie - Lineare Gleichungssysteme
	Gauß-Transformation

[vorangehende Seite] [nachfolgende Seite]

[Gesamtverzeichnis][Seitenübersicht]

Folgende Operationen lassen die Lösungsmenge eines linearen Gleichungssystems unverändert:

Vertauschung zweier Gleichungen,
Multiplikation einer Gleichung mit einem Faktor $\ne 0$ ,
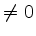Subtraktion einer Gleichung von einer anderen Gleichung.

Durch Kombination der letzten beiden Operationen ist auch die Addition eines Vielfachen einer Zeile zu einer anderen Zeile eine zulässige Operation.

Mit Hilfe dieser sogenannten Gauß-Transformation lassen sich sukzessive Unbekannte eliminieren und ein lineares Gleichungssystem auf Dreiecksform transformieren und dann durch Rückwärtseinsetzen lösen.

Um das lineare Gleichungssystem

$\begin{displaymath} \begin{array}{rcrcrcl} &-& 2x_2 &+& 5x_3 &=& 7 \\ -8x_1 &-& 4x_2 && &=& -12 \\ 4x_1 &+& 3x_2 &+& x_3 &=& 6 \end{array}\end{displaymath}$

mit Gauß-Transformationen auf Dreiecksform zu bringen, werden zunächst die erste und die dritte Zeile vertauscht:

$\begin{displaymath} \begin{array}{rcrcrcl} 4x_1 &+& 3x_2 &+& x_3 &=& 6 \\ -8x_1 &-& 4x_2 && &=& -12 \\ &-& 2x_2 &+& 5x_3 &=& 7 \,. \end{array}\end{displaymath}$

Durch Addition der mit dem Faktor 2 multiplizierten ersten Gleichung zur zweiten Gleichung erhält man

$\begin{displaymath} \begin{array}{rcrcrcl} 4x_1 &+& 3x_2 &+& x_3 &=& 6 \\ && 2x_2 &+& 2x_3&=& 0 \\ &-& 2x_2 &+& 5x_3 &=& 7 \,. \end{array}\end{displaymath}$

Addition der zweiten Gleichung zur dritten Gleichung ergibt schließlich die Dreiecksform

$\begin{displaymath} \begin{array}{rcrcrcl} 4x_1 &+& 3x_2 &+& x_3 &=& 6 \\ && 2x_2 &+& 2x_3&=& 0 \\ && && 7x_3 &=& 7 \,. \end{array}\end{displaymath}$

Durch Rückwärtseinsetzen können die Gleichungen nun sukzessive gelöst werden. Aus Gleichung 3 folgt

$\displaystyle x_3 = 1.$

Eingesetzt in Gleichung 2 erhält man

$\displaystyle 2x_2 + 2 \cdot 1 = 0 \quad \Longrightarrow \quad x_2 = -1.$

Schließlich liefert die Substitution der berechneten Unbekannten in die erste Gleichung

$\displaystyle 4x_1 +3(-1)+1 = 6 \quad \Longrightarrow \quad x_1 = (6 + 3 -1 )/4 = 2.$

(Autor: J. Wipper)

[vorangehende Seite] [nachfolgende Seite]

[Gesamtverzeichnis][Seitenübersicht]

automatisch erstellt am 23.10.2009